主題
Search

黎曼 Zeta 函式

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本
RiemannZeta

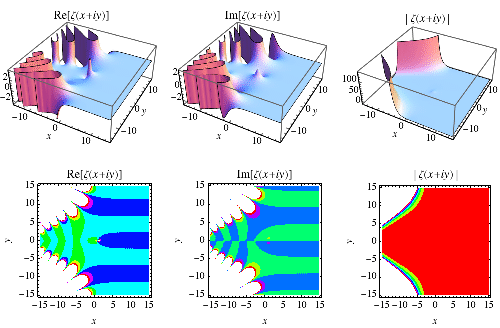
黎曼zeta函式是一個極其重要的數學和物理學特殊函式，它出現在定積分中，並與圍繞素數定理的非常深刻的結果密切相關。雖然已經研究了該函式的許多性質，但仍然存在重要的基本猜想（最著名的是黎曼猜想）至今仍未得到證明。黎曼zeta函式用 zeta(s) 表示，並在上方沿實軸繪製（使用兩種不同的比例）。

RiemannZetaReImAbs
最小值 最大值
實部 (Re)
虛部 (Im) Powered by webMathematica

一般來說，zeta(s) 是在複平面上為一個復變數定義的，該復變數通常用 s (而不是常用的 z) 表示，以尊重黎曼在其 1859 年的論文中使用的符號，該論文奠定了對該函式的研究基礎 (Riemann 1859)。

zeta(s) 在 Wolfram 語言 中實現為Zeta[s]。

RiemannZetaRidges

上面的圖顯示了 |zeta(x+iy)| 的“脊線”，對於 0<x<1 和 1<y<100。脊線對於 0<=x<=1/2 似乎單調遞減這一事實並非巧合，因為事實證明，單調遞減意味著 黎曼猜想 (Zvengrowski 和 Saidak 2003; Borwein 和 Bailey 2003, pp. 95-96)。

在 實數線 上，當 x>1 時，黎曼zeta函式可以透過積分定義為

zeta(x)=1/(Gamma(x))int_0^infty(u^(x-1))/(e^u-1)du,
(1)

其中 Gamma(x) 是 伽瑪函式。如果 x 是一個整數 n，那麼我們有恆等式

(u^(n-1))/(e^u-1)=(e^(-u)u^(n-1))/(1-e^(-u))
(2)
=e^(-u)u^(n-1)sum_(k=0)^(infty)e^(-ku)
(3)
=sum_(k=1)^(infty)e^(-ku)u^(n-1),
(4)

所以

int_0^infty(u^(n-1))/(e^u-1)du=sum_(k=1)^inftyint_0^inftye^(-ku)u^(n-1)du.
(5)

為了評估 zeta(n)，設 y=ku，使得 dy=kdu，並將上述恆等式代入以獲得

zeta(n)=1/(Gamma(n))sum_(k=1)^(infty)int_0^inftye^(-ku)u^(n-1)du
(6)
=1/(Gamma(n))sum_(k=1)^(infty)int_0^inftye^(-y)(y/k)^(n-1)(dy)/k
(7)
=1/(Gamma(n))sum_(k=1)^(infty)1/(k^n)int_0^inftye^(-y)y^(n-1)dy.
(8)

對 (8) 中的最終表示式積分得到 Gamma(n)，它抵消了因子 1/Gamma(n)，並給出了黎曼zeta函式的最常見形式，

zeta(n)=sum_(k=1)^infty1/(k^n),
(9)

有時被稱為 p-級數。

黎曼zeta函式也可以用 多重積分 定義為

zeta(n)=int_0^1...int_0^1_()_(n)(product_(i=1)^(n)dx_i)/(1-product_(i=1)^(n)x_i),
(10)

並作為 梅林變換 定義為

int_0^inftyfrac(1/t)t^(s-1)dt=-(zeta(s))/s
(11)

對於 0<R[s]<1，其中 frac(x) 是小數部分 (Balazard 和 Saias 2000)。

它出現在 單位正方形積分 中

int_0^1int_0^1([-ln(xy)]^s)/(1-xy)dxdy=Gamma(s+2)zeta(s+2),
(12)

對於 R[s]>1 有效 (Guillera 和 Sondow 2005)。對於 s 為非負整數，此公式歸功於 Hadjicostas (2002)，特殊情況 s=0 和 s=1 歸功於 Beukers (1979)。

請注意，zeta 函式 zeta(s) 在 s=1 處有一個奇點，在該點它簡化為發散的 調和級數。

黎曼zeta函式滿足反射函式方程

zeta(1-s)=2(2pi)^(-s)cos(1/2spi)Gamma(s)zeta(s)
(13)

(Hardy 1999, p. 14; Krantz 1999, p. 160)，尤拉對實數 s 猜想了一個類似的形式 (Euler, 1749 年宣讀，1768 年出版; Ayoub 1974; Havil 2003, p. 193)。這個函式方程的對稱形式由下式給出

Gamma(s/2)pi^(-s/2)zeta(s)=Gamma((1-s)/2)pi^(-(1-s)/2)zeta(1-s)
(14)

(Ayoub 1974)，黎曼為所有複數 s 證明了這一點 (Riemann 1859)。

如上定義，zeta 函式 zeta(s)，其中 s=sigma+it 是一個複數，定義域為 R[s]>1。然而，zeta(s) 具有唯一的解析延拓到整個複平面，除了點 s=1，它對應於簡單極點，復殘數為 1 (Krantz 1999, p. 160)。特別地，當 s->1 時，zeta(s) 服從

lim_(s->1)[zeta(s)-1/(s-1)]=gamma,
(15)

其中 gamma 是 尤拉-馬歇羅尼常數 (Whittaker 和 Watson 1990, p. 271)。

為了對 R[s]>0 執行解析延拓，寫成

sum_(n=1)^(infty)((-1)^n)/(n^s)+sum_(n=1)^(infty)1/(n^s)=2sum_(n=2,4,...)^(infty)1/(n^s)
(16)
=2sum_(k=1)^(infty)1/((2k)^s)
(17)
=2^(1-s)sum_(k=1)^(infty)1/(k^s),
(18)

因此，用 zeta(s) 重寫立即得到

sum_(n=1)^infty((-1)^n)/(n^s)+zeta(s)=2^(1-s)zeta(s).
(19)

因此，

zeta(s)=1/(1-2^(1-s))sum_(n=1)^infty((-1)^(n-1))/(n^s).
(20)

這裡，右側的和正是 狄利克雷eta函式 eta(s) (有時也稱為交錯zeta函式)。雖然這個公式僅為右半平面 R[s]>0 定義了 zeta(s)，但方程 (◇) 可用於將其解析延拓到複平面的其餘部分。解析延拓也可以使用 漢克爾函式 進行。黎曼zeta函式的全域性收斂級數（提供 zeta(s) 到整個複平面（除了 s=1）的解析延拓）由下式給出

zeta(s)=1/(1-2^(1-s))sum_(n=0)^infty1/(2^(n+1))sum_(k=0)^n(-1)^k(n; k)(k+1)^(-s)
(21)

(Havil 2003, p. 206)，其中 (n; k) 是一個二項式係數，這是 Knopp 在 1930 年左右提出的猜想，由 Hasse (1930) 證明，並由 Sondow (1994) 重新發現。這個方程與重整化和隨機變數有關 (Biane et al. 2001)，可以透過應用 尤拉級數變換，其中 n=0 到方程 (20) 推匯出來。

Hasse (1930) 還證明了相關的全域性（但更慢）收斂級數

zeta(s)=1/(s-1)sum_(n=0)^infty1/(n+1)sum_(k=0)^n(-1)^k(n; k)(k+1)^(1-s)
(22)

與 (21) 不同，它也可以擴充套件到黎曼zeta函式的推廣，稱為 赫爾維茨zeta函式 zeta(s,a)。zeta(s,a) 定義為使得

zeta(s)=zeta(s,1).
(23)

(如果從 zeta(s,a) 的求和定義中排除奇異項，那麼 zeta(s)=zeta(s,0) 也成立。) 將 zeta(s) 在 s=1 附近展開得到

zeta(s)=1/(s-1)+sum_(n=0)^infty((-1)^n)/(n!)gamma_n(s-1)^n,
(24)

其中 gamma_n 是所謂的 斯蒂爾傑斯常數。

RiemannZetaFunctionGamma

黎曼zeta函式也可以透過輪廓積分在複平面上定義為

zeta(z)=(Gamma(1-z))/(2pii)∮_gamma(u^(z-1))/(e^(-u)-1)du
(25)

對於所有 z!=1，其中輪廓如上圖所示 (Havil 2003, pp. 193 和 249-252)。

zeta(s) 的零點至少有兩種不同的型別。所謂的“平凡零點”出現在所有負偶數整數 s=-2、-4、-6、...，而“非平凡零點”出現在某些

s=sigma+it
(26)

對於 s 在“臨界帶” 0<sigma<1 中。黎曼猜想斷言，zeta(s) 的非平凡黎曼zeta函式零點都具有實部 sigma=R[s]=1/2，這條線稱為“臨界線”。現在已知對於前 250×10^9 個根是正確的。

RiemannZetaCriticalStrip

上面的圖顯示了 zeta(1/2+iy) 的實部和虛部（即，zeta(z) 沿臨界線的值），當 y 從 0 變化到 35 時 (Derbyshire 2004, p. 221)。

黎曼zeta函式可以分解為

zeta(1/2+it)=Z(t)e^(-itheta(t)),
(27)

其中 Z(t) 和 theta(t) 是 黎曼-西格爾函式。

黎曼zeta函式與狄利克雷lambda函式 lambda(nu) 和狄利克雷eta函式 eta(nu) 相關，關係如下：

(zeta(nu))/(2^nu)=(lambda(nu))/(2^nu-1)=(eta(nu))/(2^nu-2)
(28)

和

zeta(nu)+eta(nu)=2lambda(nu)
(29)

(Spanier 和 Oldham 1987)。

它與劉維爾函式 lambda(n) 相關，關係如下：

(zeta(2s))/(zeta(s))=sum_(n=1)^infty(lambda(n))/(n^s)
(30)

(Lehman 1960, Hardy 和 Wright 1979)。此外，

(zeta^2(s))/(zeta(2s))=sum_(n=1)^infty(2^(omega(n)))/(n^s),
(31)

其中 omega(n) 是 n 的不同質因數的數量 (Hardy 和 Wright 1979, p. 254)。

對於 -2n 為正偶數整數 -2、-4、...，

zeta^'(-2n)=((-1)^nzeta(2n+1)(2n)!)/(2^(2n+1)pi^(2n)),
(32)

給出前幾個值為

zeta^'(-2)=-(zeta(3))/(4pi^2)
(33)
zeta^'(-4)=(3zeta(5))/(4pi^4)
(34)
zeta^'(-6)=-(45zeta(7))/(8pi^6)
(35)
zeta^'(-8)=(315zeta(9))/(4pi^8)
(36)

(OEIS A117972 和 A117973)。對於 n=-1，

zeta^'(-1)=1/(12)-lnA,
(37)

其中 A 是 格萊舍-金凱林常數。使用方程 (◇) 得到導數

zeta^'(0)=-1/2ln(2pi),
(38)

它可以直接從 沃利斯公式 推匯出來 (Sondow 1994)。zeta^'(0)/zeta(0)=ln(2pi) 也可以直接從尤拉-麥克勞林求和公式推匯出來 (Edwards 2001, pp. 134-135)。一般來說，zeta^((n))(0) 可以用 pi、zeta(n)、尤拉-馬歇羅尼常數 gamma 和 斯蒂爾傑斯常數 gamma_i 解析地表示，前幾個例子是

zeta^('')(0)=gamma_1+1/2gamma^2-1/(24)pi^2-1/2[ln(2pi)]^2
(39)
zeta^(''')(0)=3ln(2pi)gamma_1+3gammagamma_1+3/2gamma_2-zeta(3)-1/2[ln(2pi)]^3-1/8pi^2ln(2pi)+3/2gamma^2ln(2pi)+gamma^3.
(40)

導數 zeta^((n))(1/2) 也可以用封閉形式給出，例如，

zeta^'(1/2)=1/4[(pi+2gamma+6ln2+2lnpi)zeta(1/2)]
(41)
=-3.92264613...
(42)

(OEIS A114875)。

對於 R[s]>1，黎曼zeta函式的導數定義為

zeta^'(s)=-sum_(k=1)^(infty)(lnk)/(k^s)
(43)
=-sum_(k=2)^(infty)(lnk)/(k^s).
(44)

zeta^'(2) 可以用封閉形式給出為

zeta^'(2)=1/6pi^2[gamma+ln(2pi)-12lnA]
(45)
=-0.93754825431...
(46)

(OEIS A073002)，其中 A 是 格萊舍-金凱林常數（由 Glaisher 1894 以級數形式給出）。

zeta^'(s) 在 s=1 附近的級數為

zeta^'(s)=-1/((s-1)^2)-gamma_1+gamma_2(s-1)-1/2gamma_3(s-1)^2+...,
(47)

其中 gamma_i 是 斯蒂爾傑斯常數。

1739 年，尤拉找到了 zeta(2n)=Cpi^(2n) 中 C 的有理係數，以 伯努利數 表示。當與林德曼在 1882 年證明 pi 是超越數相結合時，有效地證明了 zeta(2n) 是超越數。對 zeta(2n+1) 的研究要困難得多。Apéry (1979) 最終證明 zeta(3) 是無理數，但對於其他奇數 n，尚不清楚是否有類似的結果。由於 Apéry 的重要發現，zeta(3) 有時被稱為 Apéry 常數。Rivoal (2000) 以及 Ball 和 Rivoal (2001) 證明，存在無限多個整數 n，使得 zeta(2n+1) 是無理數，並且隨後證明了 zeta(5)、zeta(7)、...、zeta(21) 中至少有一個是無理數 (Rivoal 2001)。Zudilin (2001) 隨後收緊了這一結果，他表明 zeta(5)、zeta(7)、zeta(9) 或 zeta(11) 中至少有一個是無理數。

許多關於 zeta(n) 的有趣求和公式，其中 n 是一個正整數，可以用二項式係數寫成二項式和

zeta(2)=3sum_(k=1)^(infty)1/(k^2(2k; k))
(48)
zeta(3)=5/2sum_(k=1)^(infty)((-1)^(k-1))/(k^3(2k; k))
(49)
zeta(4)=(36)/(17)sum_(k=1)^(infty)1/(k^4(2k; k))
(50)

(Guy 1994, p. 257; Bailey et al. 2007, p. 70)。Apéry 在 k^(-3) 上述求和公式的幫助下得出了他的結果。已經搜尋了形式為

zeta(5)=Z_5sum_(k=1)^infty((-1)^(k-1))/(k^5(2k; k))
(51)

的關係，其中 Z_5 是一個有理數或代數數，但如果 Z_5 是一個次數為 25 或更小的多項式的根，則係數的歐幾里得範數必須大於 1.24×10^(383)，並且如果 zeta(5) 是次數為 25 或更小的代數數，則係數的範數必須超過 1.98×10^(380) (Bailey et al. 2007, pp. 70-71, 更新 Bailey 和 Plouffe)。因此，對於 zeta(n)，當 n>=5 時，尚不清楚是否有這樣的求和公式。

恆等式

sum_(k=1)^(infty)1/(k^2-x^2)=sum_(n=0)^(infty)zeta(2n+2)x^(2n)
(52)
=(1-pixcot(pix))/(2x^2)
(53)
=3sum_(k=1)^(infty)1/(k^2(2k; k)(1-(x^2)/(k^2)))product_(m=1)^(k-1)(1-(4x^2)/(m^2))/(1-(x^2)/(m^2))
(54)
=(3_4F_3(1,2,1-2x,1+2x;3/2,2-x,2+x;1/4))/(2(1-x^2))
(55)

對於 x 是不等於非零整數的複數，給出了偶數正數 n 的類 Apéry 公式 (Bailey et al. 2006, pp. 72-77)。

黎曼zeta函式 zeta(2n) 可以使用輪廓積分或具有適當傅立葉級數的帕塞瓦爾定理，對偶數 n 進行解析計算。尤拉在 1737 年首次發現了一個出乎意料且重要的公式，其中涉及素數的乘積，

zeta(s)(1-2^(-s))=(1+1/(2^s)+1/(3^s)+...)(1-1/(2^s))
(56)
=(1+1/(2^s)+1/(3^s)+...)-(1/(2^s)+1/(4^s)+1/(6^s)+...)
(57)
zeta(s)(1-2^(-s))(1-3^(-s))=(1+1/(3^s)+1/(5^s)+1/(7^s)+...)-(1/(3^s)+1/(9^s)+1/(15^s)+...)
(58)
zeta(s)(1-2^(-s))(1-3^(-s))...(1-p_n^(-s))...=zeta(s)product_(n=1)^(infty)(1-p_n^(-s))
(59)
=1.
(60)

這裡，每次後續乘以第 n 個素數 p_n，僅留下 p^(-s) 的冪項。因此，

zeta(s)=[product_(n=1)^infty(1-p_n^(-s))]^(-1),
(61)

這被稱為尤拉乘積公式 (Hardy 1999, p. 18; Krantz 1999, p. 159)，Derbyshire (2004, pp. 104-106) 稱之為“金鑰匙”。該公式也可以寫成

zeta(s)=(1-2^(-s))^(-1)product_(q=1; (mod 4))(1-q^(-s))^(-1)product_(r=3; (mod 4))(1-r^(-s))^(-1),
(62)

其中 q 和 r 分別是模 4 餘 1 和餘 3 的素數。

對於偶數 n>=2，

zeta(n)=(2^(n-1)|B_n|pi^n)/(n!),
(63)

其中 B_n 是一個伯努利數 (Mathews 和 Walker 1970, pp. 50-53; Havil 2003, p. 194)。伯努利數的另一個密切聯絡由下式提供

B_n=(-1)^(n+1)nzeta(1-n)
(64)

對於 n>=1，可以寫成

B_n=-nzeta(1-n)
(65)

對於 n>=2。（在這兩種情況下，只有偶數情況才有趣，因為對於奇數 n，B_n=0 平凡地成立。）重寫 (65)，

zeta(-n)=-(B_(n+1))/(n+1)
(66)

對於 n=1, 3, ... (Havil 2003, p. 194)，其中 B_n 是一個伯努利數，前幾個值是 -1/12、1/120、-1/252、1/240、... (OEIS A001067 和 A006953)。

雖然對於奇數 n，zeta(n) 沒有已知的解析形式，

zeta(3)=1/2sum_(k=1)^infty(H_k)/(k^2),
(67)

其中 H_k 是一個調和數 (Stark 1974)。此外，zeta(n) 可以表示為求和極限

zeta(n)=lim_(x->infty)1/((2x+1)^n)sum_(k=1)^x[cot(k/(2x+1))]^n
(68)

對於 n=3、5、... (Apostol 1973, Stark 1974 年給出的不正確)。

對於 mu(n) 莫比烏斯函式，

1/(zeta(s))=sum_(n=1)^infty(mu(n))/(n^s)
(69)

(Havil 2003, p. 209)。

zeta(n) 對於小的正整數值 n 的值是

zeta(1)=infty
(70)
zeta(2)=(pi^2)/6
(71)
zeta(3)=1.2020569032...
(72)
zeta(4)=(pi^4)/(90)
(73)
zeta(5)=1.0369277551...
(74)
zeta(6)=(pi^6)/(945)
(75)
zeta(7)=1.0083492774...
(76)
zeta(8)=(pi^8)/(9450)
(77)
zeta(9)=1.0020083928...
(78)
zeta(10)=(pi^(10))/(93555).
(79)

尤拉給出了 zeta(2) 到 zeta(26) 的值，對於偶數 n (Wells 1986, p. 54)，而 Stieltjes (1993) 在 1887 年確定了 zeta(2), ..., zeta(70) 的值，精度為 30 位小數。zeta(2n) 對於 n=1, 2, ... 的分母是 6, 90, 945, 9450, 93555, 638512875, ... (OEIS A002432)。zeta(10^n) 對於 n=0, 1, ... 的分母中的十進位制數字的數量是 1, 5, 133, 2277, 32660, 426486, 5264705, ... (OEIS A114474)。

正偶數整數的積分由下式給出

zeta(2n)=((-1)^(n+1)2^(2n-3)pi^(2n))/((2^(2n)-1)(2n-2)!)int_0^1E_(2(n-1))(x)dx,
(80)

正奇數整數的積分由下式給出

zeta(2n+1)=((-1)^n2^(2n-1)pi^(2n+1))/((2^(2n+1)-1)(2n)!)int_0^1E_(2n)(x)tan(1/2pix)dx
(81)
=((-1)^n2^(2n-1)pi^(2n+1))/((2^(2n+1)-1)(2n)!)int_0^1E_(2n)(x)cot(1/2pix)dx
(82)
=((-1)^n2^(2n)pi^(2n+1))/((2n+1)!)int_0^1B_(2n+1)(x)tan(1/2pix)dx
(83)
=((-1)^(n+1)2^(2n)pi^(2n+1))/((2n+1)!)int_0^1B_(2n+1)(x)cot(1/2pix)dx,
(84)

其中 E_n(x) 是一個尤拉多項式，B_n(x) 是一個伯努利多項式 (Cvijović 和 Klinowski 2002; J. Crepps, 私人通訊，2002 年 4 月)。

zeta(0) 的值可以透過對方程 (◇) 中的內和進行計算，其中 s=0，

zeta(0)=-sum_(n=0)^infty1/(2^(n+1))sum_(k=0)^n(-1)^k(n; k),
(85)

得到

zeta(0)=-sum_(n=0)^infty(delta_(0,n))/(2^(n+1))=-1/(2^(0+1))=-1/2,
(86)

其中 delta_(0,n) 是克羅內克delta。

類似地，zeta(-1) 的值可以透過對方程 (◇) 中的內和進行計算，其中 s=-1，

zeta(-1)=-1/3sum_(n=0)^infty1/(2^(n+1))sum_(k=0)^n(-1)^k(n; k)(k+1),
(87)

這給出了

zeta(-1)=-1/3sum_(n=0)^(infty)(delta_(0,n)-ndelta_(1,n))/(2^(n+1))
(88)
=-1/3(1/(2^(0+1))-1/(2^(1+1)))
(89)
=-1/(12).
(90)

這個值與重整化理論中的一個深刻結果有關 (Elizalde et al. 1994, 1995, Bloch 1996, Lepowski 1999)。

目前尚不清楚值

zeta(1/2)=-1.46035450880...
(91)

(OEIS A059750) 是否可以用已知的數學常數表示。例如，這個常數出現在Knuth 級數中。

拉馬努金首先發現了 zeta(n) 對於奇數 n 的快速收斂級數 (Zucker 1979, 1984, Berndt 1988, Bailey et al. 1997, Cohen 2000)。對於 n>1 且 n=3 (mod 4)，

zeta(n)=(2^(n-1)pi^n)/((n+1)!)sum_(k=0)^((n+1)/2)(-1)^(k-1)(n+1; 2k)B_(n+1-2k)B_(2k)-2sum_(k=1)^infty1/(k^n(e^(2pik)-1)),
(92)

其中 B_k 再次是伯努利數，(n; k) 是一個二項式係數。左側和式的值（除以 pi^n）在 (92) 中，對於 n=3, 7, 11, ... 分別是 7/180, 19/56700, 1453/425675250, 13687/390769879500, 7708537/21438612514068750, ... (OEIS A057866 和 A057867)。對於 n>=5 且 n=1 (mod 4), 對應的公式稍微複雜一些，

zeta(n)=((2pi)^n)/((n+1)!(n-1))sum_(k=0)^((n+1)/4)(-1)^k(n+1-4k)(n+1; 2k)B_(n+1-2k)B_(2k)-2sum_(k=1)^infty(e^(2pik)(1+(4pik)/(n-1))-1)/(k^n(e^(2pik)-1)^2)
(93)

(Cohen 2000)。

定義

S_+/-(n)=sum_(k=1)^infty1/(k^n(e^(2pik)+/-1)),
(94)

則前幾個值可以寫成

zeta(3)=7/(180)pi^3-2S_-(3)
(95)
zeta(5)=1/(294)pi^5-(72)/(35)S_-(5)-2/(35)S_+(5)
(96)
zeta(7)=(19)/(56700)pi^7-2S_-(7)
(97)
zeta(9)=(125)/(3704778)pi^9-(992)/(495)S_-(9)-2/(495)S_+(9)
(98)
zeta(11)=(1453)/(425675250)pi^(11)-2S_-(11)
(99)
zeta(13)=(89)/(257432175)pi^(13)-(16512)/(8255)S_-(13)-2/(8255)S_+(13)
(100)
zeta(15)=(13687)/(390769879500)pi^(15)-2S_-(15)
(101)
zeta(17)=(397549)/(112024529867250)pi^(17)-(261632)/(130815)S_-(17)-2/(130815)S_+(17)
(102)
zeta(19)=(7708537)/(21438612514068750)pi^(19)-2S_-(19)
(103)
zeta(21)=(68529640373)/(1881063815762259253125)pi^(21)-(4196352)/(2098175)S_-(21)-2/(2098175)S_+(21)
(104)

(Plouffe 1998)。

另一組相關公式是

zeta(3)=(pi^3)/(28)+(16)/7sum_(n=1)^(infty)1/(n^3(e^(npi)+1))-2/7sum_(n=1)^(infty)1/(n^3(e^(2pin)+1))
(105)
zeta(5)=24sum_(n=1)^(infty)1/(n^5(e^(npi)-1))-(259)/(10)sum_(n=1)^(infty)1/(n^5(e^(2pin)-1))-1/(10)sum_(n=1)^(infty)1/(n^5(e^(4pin)-1))
(106)
zeta(5)=-(7pi^5)/(1840)+(328)/(115)sum_(n=1)^(infty)1/(n^5(e^(pin)-1))-(419)/(460)sum_(n=1)^(infty)1/(n^5(e^(2pin)-1))-9/(115)sum_(n=1)^(infty)1/(n^5(e^(3pin)-1))+(261)/(1840)sum_(n=1)^(infty)1/(n^5(e^(6pin)-1))-9/(1840)sum_(n=1)^(infty)1/(n^5(e^(12pin)-1))
(107)
zeta(7)=(304)/(13)sum_(n=1)^(infty)1/(n^7(e^(pin)-1))-(103)/4sum_(n=1)^(infty)1/(n^7(e^(2pin)-1))-(19)/(52)sum_(n=1)^(infty)1/(n^7(e^(4pin)-1))
(108)
zeta(9)=(64)/3sum_(n=1)^(infty)1/(n^9(e^(pin)-1))+(441)/(20)sum_(n=1)^(infty)1/(n^9(e^(2pin)-1))-32sum_(n=1)^(infty)1/(n^9(e^(3pin)-1))-(4763)/(60)sum_(n=1)^(infty)1/(n^9(e^(4pin)-1))+(529)/8sum_(n=1)^(infty)1/(n^9(e^(6pin)-1))-1/8sum_(n=1)^(infty)1/(n^9(e^(12pin)-1))
(109)

(Plouffe 2006)。

奇數 zeta(n) 的多項和包括

zeta(5)=2sum_(k=1)^(infty)((-1)^(k+1))/(k^5(2k; k))-5/2sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((2)))/(k^3(2k; k))
(110)
zeta(7)=5/2sum_(k=1)^(infty)((-1)^(k+1))/(k^7(2k; k))+(25)/2sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((4)))/(k^3(2k; k))
(111)
zeta(9)=9/4sum_(k=1)^(infty)((-1)^(k+1))/(k^9(2k; k))-5/4sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((2)))/(k^7(2k; k))+5sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((4)))/(k^5(2k; k))+(45)/4sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((6)))/(k^3(2k; k))-(25)/4sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((2))H_(k-1)^((4)))/(k^3(2k; k))
(112)
zeta(11)=5/2sum_(k=1)^(infty)((-1)^(k+1))/(k^(11)(2k; k))+(25)/2sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((4)))/(k^7(2k; k))-(75)/4sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((8)))/(k^3(2k; k))+(125)/4sum_(k=1)^(infty)((-1)^(k+1)[H_(k-1)^((4))]^2)/(k^3(2k; k))
(113)

(Borwein 和 Bradley 1996, 1997; Bailey et al. 2007, p. 71), 其中 H_n^((r)) 是一個廣義調和數。

G. Huvent (2002) 發現了美麗的公式

zeta(5)=-(16)/(11)sum_(n=1)^infty([2(-1)^n+1]H_n)/(n^4).
(114)

許多涉及 zeta(n) 的求和恆等式包括

sum_(n=2)^(infty)[zeta(n)-1]=1
(115)
sum_(n=2,4,...)^(infty)[zeta(n)-1]=3/4
(116)
sum_(n=3,5,...)^(infty)[zeta(n)-1]=1/4
(117)
sum_(n=2)^(infty)(-1)^n[zeta(n)-1]=1/2.
(118)

涉及自變數整數倍數的和包括

sum_(n=1)^(infty)[zeta(2n)-1]=3/4
(119)
sum_(n=1)^(infty)[zeta(3n)-1]=1/3[-(-1)^(2/3)H_((3-isqrt(3))/2)+(-1)^(1/3)H_((3+isqrt(3))/2)]
(120)
sum_(n=1)^(infty)[zeta(4n)-1]=1/8(7-2cothpi),
(121)

其中 H_n 是一個調和數。

兩個令人驚訝的涉及 zeta(x) 的和由下式給出

sum_(k=2)^(infty)((-1)^kzeta(k))/k=gamma
(122)
sum_(k=2)^(infty)(zeta(k)-1)/k=1-gamma,
(123)

其中 gamma 是尤拉-馬歇羅尼常數 (Havil 2003, pp. 109 和 111-112)。方程 (122) 可以推廣到

sum_(k=2)^infty((-x)^kzeta(k))/k=xgamma+ln(x!)
(124)

(T. Drane，私人通訊，7 月 7 日，2006 年)，對於 -1<x<=1。

其他意想不到的和是

sum_(n=1)^infty(zeta(2n))/(n(2n+1)2^(2n))=lnpi-1
(125)

(Tyler 和 Chernhoff 1985; Boros 和 Moll 2004, p. 248) 和

sum_(n=1)^infty(zeta(2n))/(n(2n+1))=ln(2pi)-1.
(126)

(125) 是以下公式的特例

sum_(k=1)^infty(zeta(2k,z))/(k(2k+1)2^(2k)) =(2z-1)ln(z-1/2)-2z+1+ln(2pi)-2lnGamma(z),
(127)

其中 zeta(s,a) 是一個赫爾維茨 zeta 函式 (Danese 1967; Boros 和 Moll 2004, p. 248)。

考慮和式

S_n=sum_(k=2)^(n-2)(zeta(k)zeta(n-k))/(2^k),
(128)

則

lim_(n->infty)S_n=ln2,
(129)

其中 ln2 是 2 的自然對數，這是以下公式的特例

lim_(n->infty)sum_(k=2)^(n-2)zeta(k)zeta(n-k)x^(k-1)=x^(-1)-psi_0(-x)-gamma,
(130)

其中 psi_0(z) 是雙伽瑪函式，gamma 是尤拉-馬歇羅尼常數，可以從下式推匯出來

sum_(k=2)^inftyzeta(k)x^(k-1)=-psi_0(1-x)-gamma
(131)

(B. Cloitre，私人通訊，2005 年 12 月 11 日；參見 Borwein et al. 2000, eqn. 27)。

拉馬努金結果的推廣（他給出了 m=1 的情況）由下式給出

sum_(k=1)^infty1/([k(k+1)]^(2m+1))=-2sum_(k=0)^mzeta(2k)(4m-2k+1; 2m),
(132)

其中 (n; k) 是一個二項式係數 (B. Cloitre，私人通訊，2005 年 9 月 20 日)。

另一組關於 zeta(n) 的和由下式給出

C_1=sum_(n=2)^(infty)(zeta(n))/(n!)
(133)
=int_0^infty(I_1(2sqrt(u))-sqrt(u))/((e^u-1)sqrt(u))du
(134)
=int_0^infty(_0F^~_1(;2;u)-1)/(e^u-1)du
(135)
approx 1.078189
(136)
C_2=sum_(n=1)^(infty)(zeta(2n))/(n!)
(137)
=sum_(n=1)^(infty)e^(1/n^2)-1
(138)
=int_0^1(u_0F_2(;3/2,2;1/4u^4))/(e^u-1)du
(139)
approx 2.407447
(140)
C_3=sum_(n=1)^(infty)(zeta(2n))/((2n)!)
(141)
=int_0^infty(u+_0F^~_1(;2;-u)-_0F^~_1(;2;u))/(2(1-e^u))du
(142)
approx 0.869002.
(143)

(OEIS A093720, A076813, 和 A093721), 其中 I_n(z) 是第一類修正貝塞爾函式，_pF^~_q 是一個正則化超幾何函式。這些和沒有已知的閉式解。

RiemannZetaInv

黎曼 zeta 函式 1/zeta(p) 的倒數，如上圖所示，是 p 次方無平方數（即，無平方數，無立方數等）的漸近密度。下表給出了 Q_p(n) 個 p 次方無平方數 <=n 對於 n 的幾個值。

p1/zeta(p)Q_p(10)Q_p(100)Q_p(10^3)Q_p(10^4)Q_p(10^5)Q_p(10^6)
20.607927761608608360794607926
30.831907985833831983190831910
40.9239381093925924092395923939
50.9643871097965964596440964388
60.9829531099984983198297982954

另請參閱

阿貝爾函式方程, 貝瑞猜想, 臨界線, 臨界帶, 德拜函式, 狄利克雷 Beta 函式, 狄利克雷 Eta 函式, 狄利克雷 Lambda 函式, 尤拉乘積, 調和級數, 赫爾維茨 Zeta 函式, 辛欽常數, 萊默現象, 蒙哥馬利對相關猜想, p-級數, 週期 Zeta 函式, 素數定理, Psi 函式, 黎曼猜想, 黎曼 P 級數, 黎曼-西格爾函式, 黎曼-馮·曼戈爾特公式, 黎曼 Zeta 函式 zeta(2), 黎曼 Zeta 函式零點, 斯蒂爾傑斯常數, 沃羅寧普遍性定理, Xi 函式 在 課堂中探索此主題

相關的 Wolfram 網站

http://functions.wolfram.com/ZetaFunctionsandPolylogarithms/Zeta/

此條目部分由 Jonathan Sondow 貢獻 (作者連結)

使用 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (Eds.). "Riemann Zeta Function and Other Sums of Reciprocal Powers." §23.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.Adamchik, V. S. 和 Srivastava, H. M. "Some Series of the Zeta and Related Functions." Analysis 18, 131-144, 1998. Aizenberg, L.; Adamchik, V.; 和 Levit, V. E. "Approaching the Riemann Hypothesis with Mathematica." http://library.wolfram.com/infocenter/Articles/3268/.Apéry, R. "Irrationalité de zeta(2) et zeta(3)." Astérisque 61, 11-13, 1979.Apostol, T. M. "Another Elementary Proof of Euler's Formula for zeta(2n)." Amer. Math. Monthly 80, 425-431, 1973.Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 332-335, 1985.Ayoub, R. "Euler and the Zeta Function." Amer. Math. Monthly 81, 1067-1086, 1974.Bailey, D. H. "Multiprecision Translation and Execution of Fortran Programs." ACM Trans. Math. Software. To appear.Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; 和 Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.Bailey, D. H.; Borwein, J. M.; 和 Crandall, R. E. "On the Khinchin Constant." Math. Comput. 66, 417-431, 1997.Bailey, D. 和 Plouffe, S. "Recognizing Numerical Constants." http://www.cecm.sfu.ca/organics/papers/bailey/.Balazard, M. 和 Saias, E. "The Nyman-Beurling Equivalent Form for the Riemann Hypothesis." Expos. Math. 18, 131-138, 2000.Balazard, M.; Saias, E.; 和 Yor, M. "Notes sur la fonction zeta de Riemann, 2." Adv. Math. 143, 284-287, 1999.Ball, K. 和 Rivoal, T. "Irrationalité d'une infinité valeurs de la fonction zêta aux entiers impairs." Invent. Math. 146, 193-207, 2001.Berndt, B. C. Ch. 14 in Ramanujan's Notebooks, Part II. New York: Springer-Verlag, 1988.Beukers, F. "A Note on the Irrationality of zeta(2) and zeta(3)." Bull. London Math. Soc. 11, 268-272, 1979.Biane, P.; Pitman, J.; 和 Yor, M. "Probability Laws Related to the Jacobi Theta and Riemann Zeta Functions, and Brownian Excursions." Bull. Amer. Math. Soc. 38, 435-465, 2001.Bloch, S. "Zeta Values and Differential Operators on the Circle." J. Algebra 182, 476-500, 1996.Boros, G. 和 Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.Borwein, J. 和 Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 95-96 和 99-100, 2003.Borwein, D. 和 Borwein, J. "On an Intriguing Integral and Some Series Related to zeta(4)." Proc. Amer. Math. Soc. 123, 1191-1198, 1995.Borwein, J. M. 和 Bradley, D. M. "Searching Symbolically for Apéry-Like Formulae for Values of the Riemann Zeta Function." ACM SIGSAM Bull. Algebraic Sym. Manip. 30, 2-7, 1996.Borwein, J. M. 和 Bradley, D. M. "Empirically Determined Apéry-Like Formulae for zeta(4n+3)." Exp. Math. 6, 181-194, 1997.Borwein, J. M.; Bradley, D. M.; 和 Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.Choudhury, B. K. "The Riemann Zeta-Function and Its Derivatives." Proc. Roy. Soc. London Ser. A 450, 477-499, 1995.Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. http://www.math.u-bordeaux.fr/~cohen/hardylw.dvi. 2000.Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.Cvijović, D. 和 Klinowski, J. "Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments." J. Comput. Appl. Math. 142, 435-439, 2002.Danese, A. E. "Solution to Problem 1801. A Zeta-Function Identity." Amer. Math. Monthly 74, 80-81, 1967.Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.Elizalde, E. Ten Physical Applications of Spectral Zeta Functions. Berlin: Springer-Verlag, 1995.Elizalde, E.; Odintsov, S. D.; Romeo, A.; Bytsenko, A. A.; 和 Zerbini, S. Zeta Regularization Techniques With Applications. River Edge, NJ: World Scientific, 1994.Euler, L. "Remarques sur un beau rapport entre les series des puissances tant directes que réciproques." Mémoires de l'academie des sciences de Berlin 17, 83-106, 1768. Reprinted in Opera Omnia, Series 1, Vol. 15 pp. 70-90.Glaisher, J. W. L. "On the Constant which Occurs in the Formula for 1^1.2^2.3^3...n^n." Messenger Math. 24, 1-16, 1894.Guillera, J. 和 Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.Guy, R. K. "Series Associated with the zeta-Function." §F17 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 257-258, 1994.Hadjicostas, P. "Some Generalizations of Beukers' Integrals." Kyungpook Math. J. 42, 399-416, 2002.Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.Hardy, G. H. 和 Wright, E. M. "The Zeta Function." §17.2 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 245-247 和 255, 1979.Hasse, H. "Ein Summierungsverfahren für die Riemannsche Zeta-Reihe." Math. Z. 32, 458-464, 1930.Hauss, M. Verallgemeinerte Stirling, Bernoulli und Euler Zahlen, deren Anwendungen und schnell konvergente Reihen für Zeta Funktionen. Aachen, Germany: Verlag Shaker, 1995.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Howson, A. G. "Addendum to: 'Euler and the Zeta Function' (Amer. Math. Monthly 81 (1974), 1067-1086) by Raymond Ayoub." Amer. Math. Monthly 82, 737, 1975.Huvent, G. "Autour de la primitive de t^pcoth(alphat/2)." Feb. 3, 2002. http://perso.orange.fr/gery.huvent/articlespdf/Autour_primitive.pdf.Huylebrouck, D. "Similarities in Irrationality Proofs for pi, ln2, zeta(2), and zeta(3)." Amer. Math. Monthly 108, 222-231, 2001.Ivic, A. A. The Riemann Zeta-Function. New York: Wiley, 1985.Ivic, A. A. Lectures on Mean Values of the Riemann Zeta Function. Berlin: Springer-Verlag, 1991.Jones, G. A. 和 Jones, J. M. "The Riemann Zeta Function." Ch. 9 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 163-189, 1998.Karatsuba, A. A. 和 Voronin, S. M. The Riemann Zeta-Function. Hawthorne, NY: De Gruyter, 1992.Katayama, K. "On Ramanujan's Formula for Values of Riemann Zeta-Function at Positive Odd Integers." Acta Math. 22, 149-155, 1973.Keiper, J. "The Zeta Function of Riemann." Mathematica Educ. Res. 4, 5-7, 1995.Knopp, K. "4th Example: The Riemann zeta-Function." Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 51-57, 1996.Krantz, S. G. "Riemann's Zeta Function." §13.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 158-159, 1999.Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 35, 1983.Lehman, R. S. "On Liouville's Function." Math. Comput. 14, 311-320, 1960.Lepowski, J. "Vertex Operator Algebras and the Zeta Function." 29 Sep 1999. http://arxiv.org/abs/math.QA/9909178.Mathews, J. 和 Walker, R. L. Mathematical Methods of Physics, 2nd ed. Reading, MA: W. A. Benjamin/Addison-Wesley, pp. 50-53, 1970.Patterson, S. J. An Introduction to the Theory of the Riemann Zeta-Function. New York: Cambridge University Press, 1988.Pegg, E. Jr. 和 Weisstein, E. W. "Seven Mathematical Tidbits." Headline News. Nov. 8, 2004. https://mathworld.tw/news/2004-11-08/seventidbits/#3.Plouffe, S. "Identities Inspired from Ramanujan Notebooks II." Jul. 21, 1998. http://www.lacim.uqam.ca/~plouffe/identities.html.Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859. Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.Rivoal, T. "La fonction Zeta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs." Comptes Rendus Acad. Sci. Paris 331, 267-270, 2000.Rivoal, T. "Irrationalité d'au moins un des neuf nombres zeta(5), zeta(7), ..., zeta(21)." 25 Apr 2001. http://arxiv.org/abs/math.NT/0104221.Sloane, N. J. A. Sequences A001067, A002432/M4283, A006953/M2039, A057866, A057867, A059750, A073002, A076813, A093720, A093721, A114474, A114875, A117972, 和 A117973 in "The On-Line Encyclopedia of Integer Sequences."Sondow, J. "Analytic Continuation of Riemann's Zeta Function and Values at Negative Integers via Euler's Transformation of Series." Proc. Amer. Math. Soc. 120, 421-424, 1994.Spanier, J. 和 Oldham, K. B. "The Zeta Numbers and Related Functions." Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.Srivastava, H. M. "Some Simple Algorithms for the Evaluations and Representations of the Riemann Zeta Function at Positive Integer Arguments." J. Math. Anal. Appl. 246, 331-351, 2000.Stark, E. L. "The Series sum_(k=1)^(infty)k^(-s) s=2, 3, 4, ..., Once More." Math. Mag. 47, 197-202, 1974.Stieltjes, T. J. Oeuvres Complètes, Vol. 2 (Ed. G. van Dijk.) New York: Springer-Verlag, p. 100, 1993.Titchmarsh, E. C. The Zeta-Function of Riemann. London: Cambridge University Press, 1930.Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.Tyler, D. 和 Chernhoff, P. "Problem 3103. An Odd Sum Reappears." Amer. Math. Monthly 92, 507, 1985.Vardi, I. "The Riemann Zeta Function." Ch. 8 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 141-174, 1991.Wagon, S. "The Riemann Zeta Function." §10.6 in Mathematica in Action. New York: W. H. Freeman, pp. 353-362, 1991.Watkins,M. R. "Inexplicable Secrets of Creation." http://www.maths.ex.ac.uk/~mwatkins/zeta/.Weisstein, E. W. "Books about Riemann Zeta Function." http://www.ericweisstein.com/encyclopedias/books/RiemannZetaFunction.html.Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.Whittaker, E. T. 和 Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Woon, S. C. "Generalization of a Relation Between the Riemann Zeta Function and Bernoulli Numbers." 24 Dec 1998. http://arxiv.org/abs/math.NT/9812143.Zucker, I. J. "The Summation of Series of Hyperbolic Functions." SIAM J. Math. Anal. 10, 192-206, 1979.Zucker, I. J. "Some Infinite Series of Exponential and Hyperbolic Functions." SIAM J. Math. Anal. 15, 406-413, 1984.Zudilin, W. "One of the Numbers zeta(5), zeta(7), zeta(9), zeta(11) Is Irrational." Uspekhi Mat. Nauk 56, 149-150, 2001.Zvengrowski, P. 和 Saidak, F. "On the Modulus of the Riemann Zeta Function in the Critical Strip." Math. Slovaca 53, 145-172, 2003.

在 中引用

黎曼 Zeta 函式

請引用為

Sondow, Jonathan 和 Weisstein, Eric W. "黎曼 Zeta 函式。" 來自 Web 資源。 https://mathworld.tw/RiemannZetaFunction.html

學科分類