解析延拓

解析延拓（有時簡稱為“延拓”）提供了一種擴充套件定義域的方法，在該定義域上定義了複函式。最常見的應用是對於在點 附近由冪級數確定的復解析函式

(1)

這樣的冪級數展開通常僅在其收斂半徑內有效。但是，在有利的情況下（幸運的是這種情況也很常見！），函式 將具有一個冪級數展開，該展開在大於預期的收斂半徑內有效，並且此冪級數可用於在其原始定義域之外定義函式。例如，這允許將三角函式、指數函式、對數函式、冪函式和雙曲函式的定義從實線 自然地擴充套件到整個複平面 。類似地，解析延拓可以用於跨越複平面中的支割線擴充套件解析函式的值。

設 和 分別是在域 和 上的解析函式，並假設交集 非空，並且在 上 。那麼 稱為 到 的解析延拓，反之亦然（Flanigan 1983，第 234 頁）。此外，如果存在，則 到 的解析延拓是唯一的。

解析延拓的這種唯一性是一個相當驚人和極其有力的陳述。它實際上表明，知道複函式在某個有限復域中的值，就可以唯一地確定該函式在每個其他點的值。

透過解析延拓，從函式的任何一個冪級數表示開始，可以找到任意數量的其他冪級數，這些冪級數共同定義了函式在域的所有點的值。此外，可以從一個點到達任何點，而無需透過函式的奇點，並且由此獲得的所有冪級數的集合構成了函式的解析表示式（Whittaker 和 Watson 1990，第 97 頁）。

解析延拓可能導致一些有趣的現象，例如多值函式。例如，考慮平方根函式 的解析延拓。儘管此函式不是全域性良好定義的（因為每個非零數都有兩個平方根），但 在 附近具有良好定義的泰勒級數，

			(2)
			(3)

這可以用來擴充套件定義 的域。請注意，當 時， 的冪級數的收斂半徑為 1。

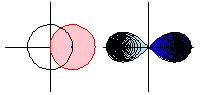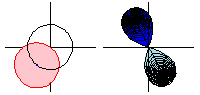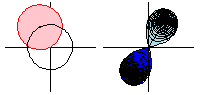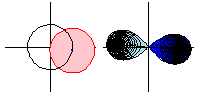
上面的動畫顯示了函式 沿路徑 的解析延拓。請注意，當函式繞一圈時， 是原始函式的負數，因此繞兩圈會將函式返回到其原始值。

在動畫中，定義域空間（粉色；左圖）透過平方根函式對映到像空間（藍色；右圖），淺藍色區域表示負平方根。但是，透過圍繞圓繼續函式，平方根函式取值在曾經是淺藍色區域的區域中，因此藍色和淺藍色區域的角色顛倒了。

這可以解釋為從多值平方根函式的一個分支到另一個分支。這說明解析延拓使用附近的提供冪級數資訊的值來擴充套件函式。

函式有可能永遠不會返回到相同的值。例如， 每次繞零點延拓時都會增加 。自然域是一個函式可以解析延拓為單值函式的最大域鏈。對於 ，它是穿孔平面的連通無限覆蓋，對於 ，它是連通雙覆蓋。如果存在函式無法擴充套件的邊界，則稱為自然邊界。例如，在單位圓盤中存在一個亞純函式 ，其中單位圓上的每個點都是極點集的極限點。那麼圓是 的自然邊界。