平方根

最小值 最大值

一個數 的平方根是一個數 ，使得 。當寫成 的形式，或者特別是 時， 的平方根也可以稱為根式或根式。因此，平方根是 n次根，其中 。

請注意，任何正實數都有兩個平方根，一個正數和一個負數。例如，9 的平方根是 和 ，因為 。任何非負實數 都有唯一的非負平方根 ；這被稱為主平方根，並寫作 或 。例如，9 的主平方根是 ，而 9 的另一個平方根是 。在通常用法中，除非另有說明，“平方根”通常指主平方根。主平方根函式 是 在 時的反函式。

最小值 最大值 實部 虛部

任何非零複數 也都有兩個平方根。例如，使用虛數單位 i， 的兩個平方根是 。數字 的主平方根表示為 (如同正實數情況)，並由 Wolfram 語言函式返回Sqrt[z].

當考慮正實數 時，可以使用 Wolfram 語言函式Surd[x, 2] 來返回實平方根。

複數 的平方根由下式給出

(1)

此外，

(2)

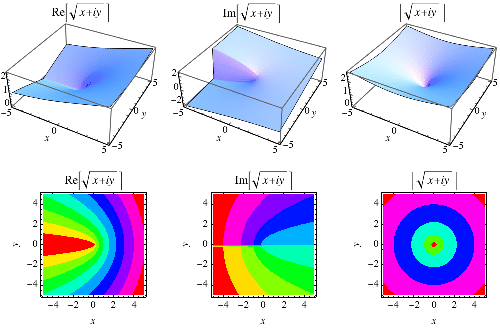
正如在上圖中可以看到的，複數平方根函式的虛部沿著負實軸有一個分支切割線。

有許多平方根演算法可以用來逼近給定（正實數）數字的平方根。這些演算法包括 Bhaskara-Brouncker 演算法和 Wolfram 迭代。最簡單的 演算法是牛頓迭代法

(3)

其中 。

2 的平方根是無理數 (OEIS A002193)，有時被稱為畢達哥拉斯常數，它具有簡單的週期連分數 [1, 2, 2, 2, 2, 2, ...] (OEIS A040000)。3 的平方根是無理數 (OEIS A002194)，有時被稱為狄奧多羅斯常數，它具有簡單的週期連分數 [1, 1, 2, 1, 2, 1, 2, ...] (OEIS A040001)。一般來說，所有正整數的平方根的連分數都是週期性的。

形如 的巢狀根式有時可以透過等式簡化為簡單的平方根

(4)

平方得到

(5)

因此

			(6)
			(7)

求解 和 得到

(8)

例如，

(9)

(10)

SimplifyWolfram 語言的 Simplify 命令不應用此類簡化，但是FullSimplify會應用此類簡化。一般來說，根式去巢狀是一個難題 (Landau 1992ab, 1994, 1998)。

反函式的反直覺性質是

(11)

因此，預期的恆等式（即， 的抵消）不沿著負實軸成立。