立方根

最小值 最大值

最小值 最大值 實部 虛部

給定一個數 ， 的立方根，記作 或 ( 的 1/3 次方)，是一個數 ，使得 。因此，立方根是 n 次根，其中 。每個實數都有唯一的實立方根，並且每個非零複數都有三個不同的立方根。

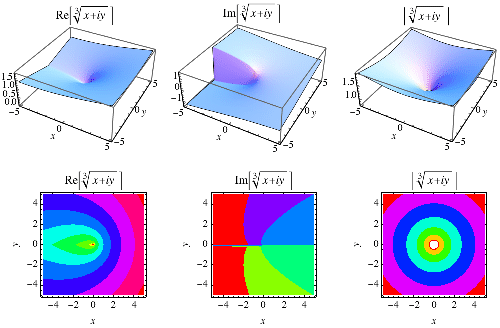
負數的立方根的教科書定義是 。然而，將立方根擴充套件到複平面會沿著負實軸產生分支切割，如上圖所示，這是立方根的主值。按照慣例，“the”（主要的）立方根因此是一個具有正虛部的複數。因此，Wolfram 語言和其他符號代數語言和程式返回在整個複平面上有效的結果，因此對於 返回複數結果。例如，在 Wolfram 語言中，ComplexExpand[(-1)^(1/3)] 給出結果 。

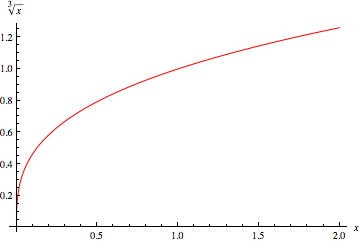
當考慮正實數 時，Wolfram 語言函式CubeRoot[x]，它等價於Surd[x, 3]，可以用來返回實立方根。

數字 的立方根可以使用牛頓法計算，透過迭代應用

對於一些實數起始值 。