冪

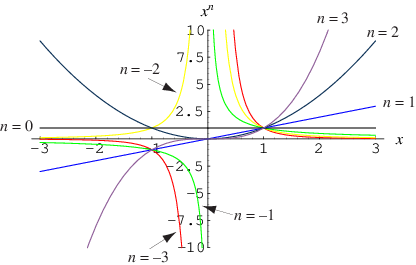
冪是指給定量的指數。表示式 因此被稱為“ 的 次冪。” 上面繪製了一些 的冪（參見 Derbyshire 2004，第 68 頁和 73 頁）。

冪可以是整數、實數 或 複數。然而，實數的非整數次冪不一定是實數本身。例如， 僅當 時為實數。

任何非 0 的數取 0 次冪都被定義為 1，這從 極限

(1)

這一事實透過上圖中曲線在 處的收斂來展示，該圖顯示了 ，其中 , 0.4, ..., 2.0。透過注意到重複對一個數 開 平方根 會得到越來越小的數，這些數從上方接近 1，而對 0 和 1 之間的數執行相同的操作會得到越來越大的數，這些數從下方接近 1，也可以更直觀地看到這一點。對於 次平方根，總冪為 ，當 很大時，它趨近於 0，在 很大的極限情況下，得到 。

（零 的零次冪）本身是未定義的。對於這個量缺乏明確定義的含義，是由於相互矛盾的事實： 始終為 1，因此 應等於 1，但 始終為 0（對於 ），因此 應等於 0。對於 的定義通常被定義為 不定式，儘管定義 可以簡化某些公式的表達（Knuth 1992；Knuth 1997，第 57 頁）。

一個數的 1 次冪，根據定義，等於它本身，即

(2)

類似地，

(3)

對於任何複數 。因此，柯克艦長（威廉·夏特納飾）能夠檢測到星艦企業號上比透過放大“1 的 4 次冪”的聽覺感測器所能解釋的心跳多一次，這令人印象深刻，這發生在第一季星際迷航劇集“軍事法庭”（1967 年）中。

組合包含冪的量的規則稱為 指數定律，將底數提升到給定冪的過程稱為 求冪。

的 導數 由下式給出

(4)

而 不定積分 由下式給出

(5)

對於實數 的 定積分 被稱為 卡瓦列裡求積公式，由下式給出

(6)

雖然簡單的方程

(7)

無法使用傳統的 初等函式 求解 ，但可以使用 Lambert W 函式 給出解，即

(8)

其中 是 的 自然對數。

類似地，方程

(9)

可以使用 Lambert W 函式 求解 ，以 表示。在特殊情況 中，除了解 和 外，第三個解是

			(10)
			(11)

（OEIS A073084）。

下表列出了各種冪的特殊名稱。

冪	名稱
	倒數
	平方根
	立方根
1	恆等函式
2	平方
3	立方

形式為 的表示式被稱為 冪塔。

數字 , 2, 3, ... 可以表示為 形式的最大冪 分別為 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, ... (OEIS A052409)，對應的 值分別為 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, ... (OEIS A052410)。

雙二項式和給出冪函式如下，

(12)

（K. MacMillan，私人通訊，2007 年 11 月 14 日）。

前 個 正整數 的 冪和 由 法烏爾哈伯公式 給出，

(13)

其中 是 克羅內克 delta， 是 二項式係數，而 是 伯努利數。

設 是不能表示為不同的 次 正 整數 的 和 的最大 整數 (Guy 1994)。, 3, ... 的前幾個值是 128, 12758, 5134240, 67898771, ... (OEIS A001661)。

卡塔蘭猜想（現在是一個定理）指出 8 和 9 ( 和 ) 是僅有的連續冪（不包括 0 和 1），即 卡塔蘭丟番圖問題 的唯一解。此外，Hyyrő 和 Makowski 證明不存在三個連續的冪 (Ribenboim 1996)。

很少有 形式為 的數是 素數（其中複合冪 不需要考慮，因為 ）。對於 和 素數 ，形式為 的唯一 素數 對應於 和 梅森素數，即 、、、...。形式為 的其他數等於 。對於 和 素數 ，形式為 的唯一 素數 對應於 ，其中 , 2, 4, 6, 10, 14, 16, 20, 24, 26, ... (OEIS A005574)。形式為 的其他數等於 。

方程

(14)

對於 沒有非平凡解 (Guy 1994, p. 153)。