 |
(1)
|
其中 
是複數輻角。 明確地用實部和虛部表示，
![(a+bi)^(c+di)=(a^2+b^2)^(c/2)e^(-darg(a+ib))×{cos[carg(a+ib)+1/2dln(a^2+b^2)]+isin[carg(a+ib)+1/2dln(a^2+b^2)]}.](/images/equations/ComplexExponentiation/NumberedEquation2.svg) |
(2)
|
複數指數運算的一個明確例子由下式給出
![(1+i)^(1+i)=sqrt(2)e^(-pi/4)[cos(1/4pi+1/2ln2)+isin(1/4pi+1/2ln2)].](/images/equations/ComplexExponentiation/NumberedEquation3.svg) |
(3)
|
一個複數取複數冪可以是實數。 事實上，著名的例子
 |
(4)
|
表明純虛數 
自乘冪是實數。
 |
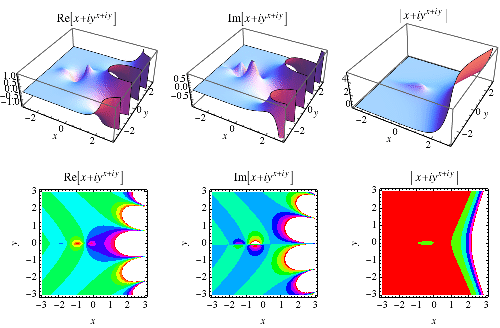事實上，存在一系列值 
使得 
是實數，正如透過以下表達式可以看出
![(ik)^(ik)=e^(-kpi/2)[cos(klnk)+isin(klnk)].](/images/equations/ComplexExponentiation/NumberedEquation5.svg) |
(5)
|
當 
時，這將是實數，即，對於
 |
(6)
|
對於 
整數。 對於正 
，這給出根 
或者
 |
(7)
|
其中 
是 Lambert W 函式。 對於 
，這簡化為
 |
(8)
|
對於 
, 2, ..., 這些給出數值 1, 2.92606 (OEIS A088928), 4.30453, 5.51798, 6.63865, 7.6969, ....
