Symmedian Point (中點)

Symmedian Point (中點) 是 的 symmedian 線 的交點，有時也稱為 Lemoine 點（在英國和法國）或 Grebe 點（在德國）。等效地，symmedian 點是 等角共軛點，是 三角形質心 的等角共軛點。換句話說，設 為 三角形 三角形 的 三角形質心，、 和 為 的中線，、 和 為 角 角平分線 、、 和 、 和 為 、 和 關於 、 和 的反射。那麼 是線條 、 和 的交點。根據 Honsberger（1995 年，第 53 頁），symmedian 點是“現代幾何的皇冠上的寶石之一”。symmedian 點是 Kimberling 中心 。

symmedian 點具有等效的 三角形中心函式 和

(1)

(Honsberger 1995, p. 75), 或

(2)

在 精確的三線性座標 中，symmedian 點是 為最小值的點 (Honsberger 1995, pp. 75-76)。一箇中心 是其自身 垂足三角形 的 三角形質心 當且僅當 它是 symmedian 點。symmedian 點是一個 三角形 及其 切線三角形 的透視中心。

下表總結了作為 Kimberling 中心的命名三角形的 symmedian 點。

三角形	Kimberling	給定三角形的 symmedian 點
反補三角形		反補三角形的 symmedian 點
外接圓弧中點三角形		和 的中點
外心-中線三角形		三線性商
外法三角形		外心
外切三角形		外心
切點三角形		Gergonne 點
D-三角形		symmedian 點
旁心三角形		Mittenpunkt
第一 Morley 三角形		第一 Morley 中心
第一 Yff 圓三角形		線 和 的交點
內 Napoleon 三角形		三角形質心
中線三角形		補點 的 symmedian 點
垂心三角形		垂心三角形的 symmedian 點
外 Napoleon 三角形		三角形質心
參考三角形		symmedian 點
第二 Yff 圓三角形		線 和 的交點
Stammler 三角形		外心
切線三角形		切線三角形的 symmedian 點
第二 Brocard 三角形		的調和點

在上面的圖中， 是 symmedian 點，

(3)

(Honsberger 1995, p. 76).

symmedian 點位於 Brocard 軸 和 Fermat 軸 上。它位於 Brocard 圓 上，並且是 餘弦圓 的中心。它也位於 Jerabek 雙曲線 和 Thomson 三次曲線 上。

它從 到 三角形 各邊的距離是

(4)

其中 是 Brocard 角。

到其他一些命名的三角形中心的距離由下式給出

			(5)
			(6)
			(7)
			(8)
			(9)

其中 是 三角形質心， 是 垂心， 是 內心， 是 mittenpunkt， 是 外心。

一條 Brocard 線、三角形中線 和 symmedian 線（每種線中的一條）是 共點 的，其中 、 和 交於一點，其中 是第一個 Brocard 點， 是 三角形質心。類似地，、 和 ，其中 是第二個 Brocard 點，交於一點，該點是第一個點的 等角共軛點 (Johnson 1929, pp. 268-269)。

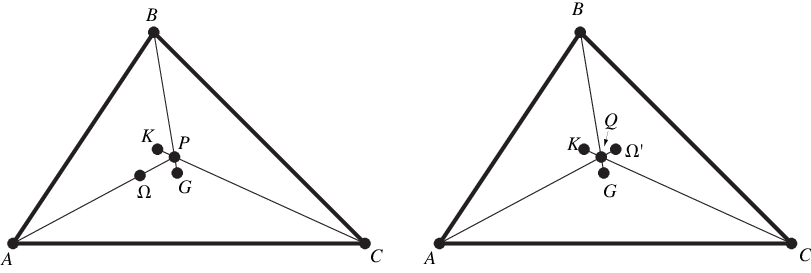
連線任意一邊的 中點 到該邊上 高 的中點的線透過 （左圖）。特別是，直角三角形 的 symmedian 點是到 斜邊 的 高 的 中點（右圖；Honsberger 1995, p. 59）。symmedian 點 是第一個 Brocard 三角形 的 Steiner 點。

給定一個三角形 ，構造三角形 ，該三角形是透過從每個頂點延伸穿過 的 symmedian 點的線與 的 外接圓 的交點獲得的。那麼 的 symmedian 點再次是 (Honsberger 1995, p. 77)。

在三角形的兩個頂點處與 外接圓 的切線相交於從第三個頂點發出的 symmedian 線 (Honsberger 1995, pp. 60-61)。三角形的 Gergonne 點 是其 切點三角形 的 symmedian 點 (Honsberger 1995, pp. 62-63)。三角形的 symmedian 點是其 垂足三角形 的 三角形質心。最後，symmedian 點的 垂足三角形 的邊長與原始三角形的 三角形中線 的長度成比例 (Honsberger 1995, p. 77)。