Brocard 點

第一 Brocard 點 是三角形 的內部點 （也記作 或 ），其中點以逆時針順序標記，使得角 、 和 相等，且唯一的這樣的角記為 。它不是一個三角形中心，但具有三線座標

(1)

（Kimberling 1998, p. 47）。

請注意，在查閱文獻時需要格外小心，因為反轉三角形頂點的標記順序會導致 Brocard 點的交換。

第二 Brocard 點 是內部點 （也記作 或 ），使得角 、 和 相等，且唯一的這樣的角記為 。它不是一個三角形中心，但具有三線座標

(2)

（Kimberling 1998, p. 47）。

此外，兩個角 相等，並且這個角被稱為Brocard 角，

			(3)
			(4)

前兩個 Brocard 點是等角共軛點（Johnson 1929, p. 266）。它們由法國陸軍軍官 Henri Brocard 於 1875 年描述，儘管 Jacobi 曾在此之前進行過研究，而 Crelle 在 1816 年也研究過（Wells 1991；Honsberger 1995, p. 98）。它們滿足

(5)

其中 是外心， 是外接圓半徑，並且 ，其中 是外心， 是Brocard 角（Honsberger 1995, p. 106）。

通常的說法（Bernhart 1959；Wells 1991, pp. 21-22；Marshall et al. 2005）歸因於 Brocard，以回應 Edouard Lucas 在 1877 年提出的問題，即如果三隻狗從三角形的頂點出發，並以恆定速度追逐它們的左鄰或右鄰，則三隻狗將在 或 處相遇，這是不正確的。透過考慮一個接近共線的等腰三角形 可以看出這一點，並注意到其中兩隻狗需要比另一隻狗走得遠得多，因此不可能以相同的速度行進（參見 Peterson 2001，Nester），以便在點 或 之一處與其他兩隻狗相遇。

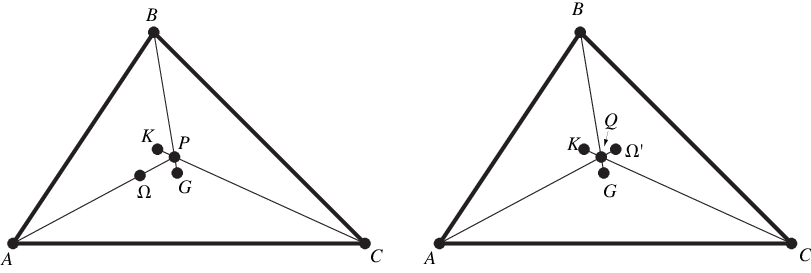
一條 Brocard 線、一條三角形中線 和一條交心線（每種線中取一條）是共點的，其中 、 和 交於一點，其中 是三角形重心， 是交心點。類似地，、 和 交於一點，該點是第一個點的等角共軛點（Johnson 1929, pp. 268-269；Honsberger 1995, pp. 121-124）。

設 是透過頂點 和 並與直線 在 處相切的圓，對於 和 也是如此。那麼圓 、 和 在第一 Brocard 點 處相交。類似地，設 是透過頂點 和 並與直線 在 處相切的圓，對於 和 也是如此。那麼圓 、 和 在第二 Brocard 點 處相交（Johnson 1929, pp. 264-265；Honsberger 1995, pp. 99-100）。

垂足三角形 和 是全等的，並且與三角形 相似（Johnson 1929, p. 269）。涉及 Brocard 點的長度包括

(6)

(7)

將線段 、 和 延伸到 的外接圓以形成 ，並將線段 、 和 延伸以形成 。那麼 和 與 全等（Honsberger 1995, pp. 104-106）。

第三 Brocard 點 透過三角形中心函式與給定的三角形相關

(8)

（Casey 1893, Kimberling 1994），並且是Kimberling 中心 。第三 Brocard 點 （或 或 ）與Spieker 中心以及其三角形的內心的等張共軛點共線。