正切函式定義為
 |
(1)
|
其中  是 正弦 函式,
是 正弦 函式, 是 餘弦 函式。符號
是 餘弦 函式。符號  有時也使用(Gradshteyn 和 Ryzhik 2000,第 xxix 頁)。
有時也使用(Gradshteyn 和 Ryzhik 2000,第 xxix 頁)。
在 直角三角形 中,角度  的正切的常見教科書定義(等同於剛剛給出的定義)是角對邊邊長與角鄰邊邊長的比率,即
的正切的常見教科書定義(等同於剛剛給出的定義)是角對邊邊長與角鄰邊邊長的比率,即
 |
(2)
|
記住 正弦、餘弦和正切定義的便捷助記符是 SOHCAHTOA (正弦 等於對邊除以斜邊,餘弦 等於鄰邊除以斜邊,正切等於對邊除以鄰邊)。
“正切”一詞也具有重要的相關含義,指在單個點接觸給定曲線或實體的 直線 或 平面。這些幾何物件然後分別稱為 切線 或 切平面。
正切函式的定義可以擴充套件到複數引數  ,使用定義
,使用定義
其中 e 是 自然對數 的底數,i 是 虛數。正切在 Wolfram 語言 中實現為Tan[z]。
一個相關的函式,稱為 雙曲正切,類似地定義為,
 |
(7)
|
一個重要的正切恆等式由下式給出
 |
(8)
|
角和、差、半形和倍角公式由下式給出
正弦 和 餘弦 函式可以方便地用正切表示為
這在多項式計算中可能特別方便,例如 Gröbner 基,因為它減少了方程的數量,與顯式包含  和
和  以及附加關係
以及附加關係  相比(Trott 2006,第 39 頁)。
相比(Trott 2006,第 39 頁)。
這些導致了漂亮的恆等式
 |
(18)
|
對於三個變數,還有一個美麗的角和恆等式,
 |
(19)
|
另一個正切恆等式是
其中  (Beeler et al. 1972)。顯式寫出,
(Beeler et al. 1972)。顯式寫出,
 |
(23)
|
這給出了前幾個展開式為
(OEIS A034867 和 A034839)。
一個推廣正切角和公式的漂亮公式,(27)和(28)由下式給出
 |
(29)
|
(Szmulowicz 2005)。
有許多基於上面給出的簡單但有趣的正切恆等式,包括
 |
(30)
|
(Borchardt 和 Perrott 1930)。
對於  有效的 麥克勞林級數 對於正切函式是
有效的 麥克勞林級數 對於正切函式是
(OEIS A002430 和 A036279),其中  是 伯努利數。
是 伯努利數。
對於任何 有理數  ,
, 是 無理數,這可以透過將
是 無理數,這可以透過將  寫成 連分數 來證明,如
寫成 連分數 來證明,如
 |
(33)
|
(Wall 1948,第 349 頁;Olds 1963,第 138 頁)和
 |
(34)
|
兩者都歸功於 Lambert。
一個有趣的涉及正切 乘積 的恆等式是
 |
(35)
|
其中  是 向下取整函式。
是 向下取整函式。
方程
 |
(36)
|
它等價於  ,其中
,其中  是 tanc 函式,沒有簡單的閉式解。
是 tanc 函式,沒有簡單的閉式解。
對於更高階的解,連續解之間的差異越來越接近  。函式
。函式  有時被稱為 tanc 函式。
有時被稱為 tanc 函式。
另請參閱
交錯排列、
餘弦、
餘切、
雙曲正切、
反切、
正切定理、
莫里定律、
正弦、
SOHCAHTOA、
Tanc 函式、
切線、
切平面、
切向量、
瓦爾迪積分 在 課堂中探索此主題
相關 Wolfram 網站
http://functions.wolfram.com/ElementaryFunctions/Tan/
使用 探索
參考文獻
Abramowitz, M. 和 Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.Beeler, M. et al. Item 16 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 9, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/recurrence.html#item16.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 226, 1987.Borchardt, W. G. 和 Perrott, A. D. Ex. 33 in A New Trigonometry for Schools. London: G. Bell, 1930.Gradshteyn, I. S. 和 Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.Olds, C. D. Continued Fractions. New York: Random House, 1963.Sloane, N. J. A. Sequences A002430/M2100, A034839, A034867, A036279, and A115365 in "The On-Line Encyclopedia of Integer Sequences."Szmulowicz, F. "New Analytic and Computational Formalism for the Band Structure of  -Layer Photonic Crystals." Phys. Lett. A 345, 469-477, 2005.Spanier, J. 和 Oldham, K. B. "The Tangent
-Layer Photonic Crystals." Phys. Lett. A 345, 469-477, 2005.Spanier, J. 和 Oldham, K. B. "The Tangent  and Cotangent
and Cotangent  Functions." Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.Tropfke, J. Teil IB, §2. "Die Begriffe von Tangens und Kotangens eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 23-28, 1923.Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.
Functions." Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.Tropfke, J. Teil IB, §2. "Die Begriffe von Tangens und Kotangens eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 23-28, 1923.Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.在 上被引用
正切
請引用為
Weisstein, Eric W. "正切。" 來源 Web 資源。 https://mathworld.tw/Tangent.html
學科分類
是 正弦 函式,
是 餘弦 函式。符號
有時也使用(Gradshteyn 和 Ryzhik 2000,第 xxix 頁)。
的正切的常見教科書定義(等同於剛剛給出的定義)是角對邊邊長與角鄰邊邊長的比率,即
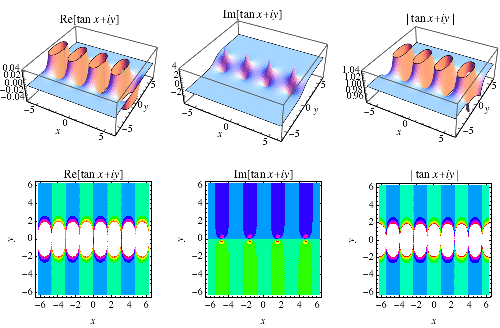
,使用定義



和
以及附加關係
相比(Trott 2006,第 39 頁)。


(Beeler et al. 1972)。顯式寫出,

有效的 麥克勞林級數 對於正切函式是

是 伯努利數。
,
是 無理數,這可以透過將
寫成 連分數 來證明,如



是 向下取整函式。
,其中
是 tanc 函式,沒有簡單的閉式解。
。函式
有時被稱為 tanc 函式。