向下取整函式

向下取整函式 , 也被稱為最大整數函式或整數值 (Spanier and Oldham 1987), 給出小於或等於 的最大整數。向下取整函式的名稱和符號由 K. E. Iverson (Graham et al. 1994) 創造。

不幸的是，在許多較舊和當前的作品中 (例如，Honsberger 1976, p. 30; Steinhaus 1999, p. 300; Shanks 1993; Ribenboim 1996; Hilbert and Cohn-Vossen 1999, p. 38; Hardy 1999, p. 18)，符號 被用來代替 (Graham et al. 1994, p. 67)。 事實上，這種表示法可以追溯到高斯在 1808 年對二次互反律的第三次證明。然而，由於向下取整函式和向上取整函式符號 和 的優雅對稱性，並且由於 在被解釋為 Iverson 括號時是一個非常有用的符號，因此應該棄用使用 來表示向下取整函式。 在這項工作中，符號 被用來表示最接近的整數函式，因為它自然地落在 和 符號之間。

最小值 最大值 實部 虛部

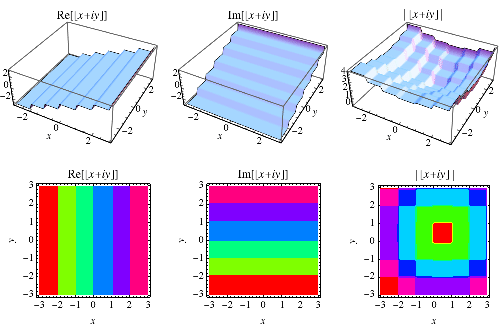
向下取整函式在 Wolfram 語言中實現為Floor[z]，其中它被推廣到複數值 ，如上所示。

由於關於小數部分/值和整數部分/值的用法可能會令人困惑，下表總結了使用的名稱和符號。這裡，S&O 表示 Spanier 和 Oldham (1987)。

符號	名稱	S&O	Graham 等人	Wolfram 語言
	向上取整函式	--	向上取整，最小整數	Ceiling[x]
	同餘	--	--	Mod[m, n]
	向下取整函式		向下取整，最大整數，整數部分	Floor[x]
	小數數值		小數部分或	SawtoothWave[x]
	小數部分		無名稱	FractionalPart[x]
	整數部分		無名稱	IntegerPart[x]
	最接近的整數函式	--	--	Round[x]
	商	--	--	Quotient[m, n]

向下取整函式滿足以下恆等式

(1)

對於所有整數 。

許多分子中帶有向下取整函式的類幾何序列可以進行解析計算。例如，以下形式的和

(2)

對於有理數 可以進行解析計算。對於 單位分數，

(3)

這種形式的和導致類似魔鬼階梯的行為。

對於無理數 ，連分數收斂 ，以及 ,

(4)

（Borwein et al. 2004, p. 12）。這引出了一個相當驚人的結果，將 alpha 倍數的向下取整函式之和與 alpha 的連分數聯絡起來，透過

(5)

（Mahler 1929；Borwein et al. 2004, p. 12）。