向上取整函式

函式 給出小於或等於 整數 的最小值，如上圖粗曲線所示。Schroeder (1991) 將向上取整函式符號稱為“絞刑架”，因為其外觀與用於絞刑的結構相似。向上取整函式的名稱和符號是由 K. E. Iverson (Graham et al. 1994) 創造的。

最小值 最大值 實部 虛部

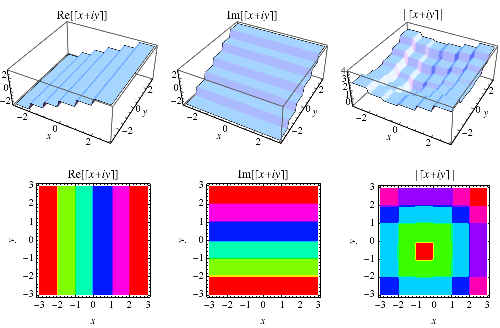向上取整函式在 Wolfram 語言中實現為Ceiling[z]，其中它被推廣到複數值 ，如上圖所示。

儘管一些作者使用符號 來表示向上取整函式（類比於較舊的符號 表示向下取整函式），但不鼓勵這種做法（Graham et al. 1994, p. 67）。同樣強烈不鼓勵使用符號 來表示向上取整函式（例如，Harary 1994，第 91、93 和 118-119 頁），因為這個符號更常用於表示 小數部分 。

由於關於小數部分/值和整數部分/值的用法可能會令人困惑，下表總結了使用的名稱和符號。此處，S&O 指的是 Spanier 和 Oldham (1987)。

符號	名稱	S&O	Graham et al.	Wolfram 語言
	向上取整函式	--	向上取整，最小整數	Ceiling[x]
	同餘	--	--	Mod[m, n]
	向下取整函式		向下取整，最大整數，整數部分	Floor[x]
	小數值		小數部分 或	SawtoothWave[x]
	小數部分		無名稱	FractionalPart[x]
	整數部分		無名稱	IntegerPart[x]
	最近整數函式	--	--	Round[x]
	商	--	--	Quotient[m, n]