最接近整數函式

最接近整數函式，也稱為 nint 或 round 函式，定義為 是最接近 的整數。 雖然符號 有時用於表示最接近整數函式（Hastad等人，1988），但這種符號相當笨拙，不建議使用。 另請注意，雖然 有時用於表示最接近整數函式，但 也常用於表示向下取整函式 （包括高斯在他 1808 年對二次互易律的第三次證明中），因此也不鼓勵使用這種符號。

由於對於半整數，定義是模稜兩可的，因此通常會新增額外的規則，即半整數總是四捨五入到偶數，以避免統計偏差。 例如，，，，，等等。 C 中遵循此約定math.h庫函式rint，以及 Wolfram 語言，其中最接近整數函式實現為Round[x]。

由於關於小數部分/值和整數部分/值的用法可能令人困惑，下表總結了使用的名稱和符號。 此處，S&O 表示 Spanier 和 Oldham (1987)。

符號	名稱	S&O	Graham 等人	Wolfram 語言
	向上取整函式	--	向上取整，最小整數	Ceiling[x]
	同餘	--	--	Mod[m, n]
	向下取整函式		向下取整，最大整數，整數部分	Floor[x]
	小數數值		小數部分 或	SawtoothWave[x]
	小數部分		無名稱	FractionalPart[x]
	整數部分		無名稱	IntegerPart[x]
	最接近整數函式	--	--	Round[x]
	商	--	--	Quotient[m, n]

上面的圖說明了對於小的 的 。

Min Max Re Im

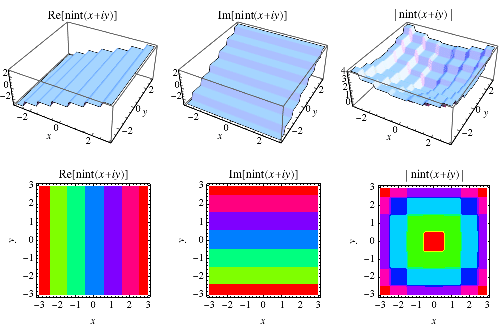最接近整數函式也可以擴充套件到複平面，如上圖所示。