在老鼠問題中,也稱為甲蟲問題, 只老鼠從單位邊長的正
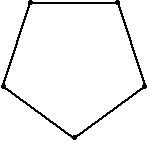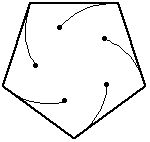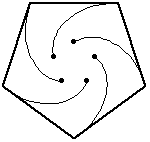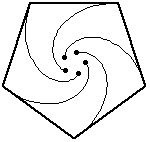
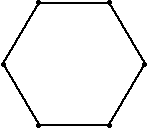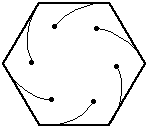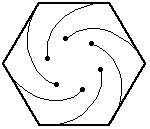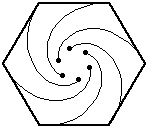
只老鼠從單位邊長的正  -邊形的角開始,每隻老鼠都以恆定速度朝逆時針方向最近的鄰居老鼠移動。老鼠們各自追蹤一條對數螺線,在多邊形的中心相遇,並移動了一段距離
-邊形的角開始,每隻老鼠都以恆定速度朝逆時針方向最近的鄰居老鼠移動。老鼠們各自追蹤一條對數螺線,在多邊形的中心相遇,並移動了一段距離
n= , 3, ... 的前幾個值是
, 3, ... 的前幾個值是
給出的數值為 0.5, 0.666667, 1, 1.44721, 2, 2.65597, 3.41421, 4.27432, 5.23607, .... 連線老鼠在等時間間隔位置形成的曲線是一個吸引人的圖形,稱為漩渦線。
這個問題也被不同地稱為(三隻、四隻等)(蟲子、狗等)問題。它可以推廣到不規則多邊形和以不同速度移動的老鼠(Bernhart 1959)。Miller (1871) 考慮了三隻處於一般位置的老鼠,並調整速度以保持路徑相似,且三角形與原始三角形相似。
另請參閱
阿波羅尼斯追逐問題,
布羅卡點,
追蹤曲線,
螺線,
曳物線,
漩渦線
使用 探索
參考文獻
Bernhart, A. "追逐多邊形。" Scripta Math. 24, 23-50, 1959.Brocard, H. "盧卡斯問題的解。" Nouv. Corresp. Math. 3, 280, 1877.Clapham, A. J. Rec. Math. Mag., Aug. 1962.Gardner, M. 科學美國人數學謎題和消遣書。 New York: NY: Simon and Schuster, 1959.Gardner, M. 科學美國人數學遊戲第六輯。 Chicago, IL: University of Chicago Press, pp. 240-243, 1984.Good, I. J. "追蹤曲線和數學藝術。" Math. Gaz. 43, 34-35, 1959.Lucas, E. "三狗問題。" Nouv. Corresp. Math. 3, 175-176, 1877.Madachy, J. S. Madachy 的數學娛樂。 New York: Dover, pp. 201-204, 1979.Marshall, J. A.; Broucke, M. E.; and Francis, B. A. "獨輪車的追逐隊形。" Automata 41, 2005. http://www.control.toronto.edu/~marshall/docs/MarBroFra-Auto-4141-final.pdf.Miller, R. K. Problem 16. Cambridge Math. Tripos Exam. January 5, 1871.Nester, D. "數學研討會:三角形的甲蟲中心。" http://www.bluffton.edu/mat/dept/seminar_docs/BeetleCenters/.Steinhaus, H. 數學快照,第三版。 New York: Dover, p. 136, 1999.Wells, D. 企鵝好奇和有趣的幾何學詞典。 London: Penguin, pp. 201-202, 1991.Wilson, J. "問題:四隻狗。" http://jwilson.coe.uga.edu/emt725/Four.Dogs/four.dogs.html.在 中被引用
老鼠問題
請引用為
Weisstein, Eric W. "老鼠問題。" 來自 ——Wolfram 網路資源。 https://mathworld.tw/MiceProblem.html
學科分類
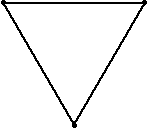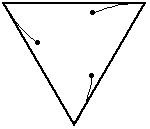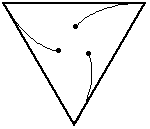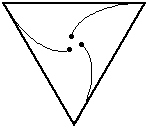

只老鼠從單位邊長的正
-邊形的角開始,每隻老鼠都以恆定速度朝逆時針方向最近的鄰居老鼠移動。老鼠們各自追蹤一條對數螺線,在多邊形的中心相遇,並移動了一段距離

, 3, ... 的前幾個值是
