主題
Search

追逐曲線

下載 Mathematica Notebook下載 Wolfram 筆記本

如果 A 沿著已知曲線移動，那麼如果 P 始終朝向 A 且 A 和 P 以勻速運動，則 P 描述了一條追逐曲線。法國科學家皮埃爾·布格在 1732 年首次普遍考慮了追逐曲線，隨後英國數學家布林也進行了研究。

在電視劇NUMB3RS 第二季劇集 "Dark Matter" 中，數學天才查理·埃普斯在考慮神秘的第三名槍手的行動時，以 “路徑最小化” 的名義提到了追逐曲線。

追逐方程由下式給出

(A-P)/(|A-P|)·(P^.)/(|P^.|)=1,
(1)

它指定了點 P 處的 切向量 始終平行於連線 A 和 P 的直線，並結合

P^.·P^.=1,
(2)

它指定了點 P 以恆定速度移動（不失一般性，在上面取為單位速度）。因此，將 (2) 代入 (1) 得出

((A-P)·P^.)/(|A-P|)=1.
(3)
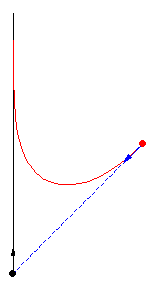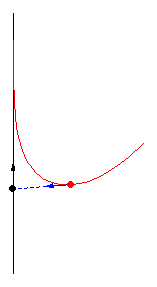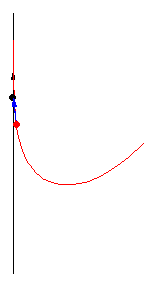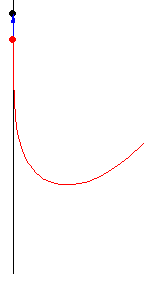
Pursuit curve for a straight vertical path

亞瑟·伯恩哈特（MacTutor Archive）研究了限制 A 為直線的案例。取 A(t)=(0,t) 的引數方程和點 P 的方程為 P=(x,y)，則此問題的運動方程由下式給出

1/(sqrt(x^2+(t-y)^2))[0-x; t-y]·[x^.; y^.]=1
(4)

和

x^.^2+y^.^2=1.
(5)

對 (4) 進行平方和重新排列得到

[(t-y)y^.-xx^.]^2=x^2+(t-y)^2.
(6)

展開得到

x^2(x^.^2-1)+2x(y-t)x^.y^.+(t-y)^2(y^.^2-1)=0,
(7)

可以使用 (5) 將其簡化為

x^2y^.^2+2x(t-y)x^.y^.+(t-y)^2x^.^2=0.
(8)

但這是一個完全平方

[xy^.+(t-y)x^.]^2=0,
(9)

因此，對兩邊取平方根得到

xy^.+(t-y)x^.=0.
(10)

可以透過將兩邊除以 x^.，將此方程轉換為 y 作為 x 函式的方程，得到

xy^'+t-y=0,
(11)

其中 y^'=y^./x^.=(dy/dt)/(dx/dt)=dy/dx。為了消除 t，請注意 P 行駛的弧長由下式給出

s=intsqrt(1+y^('2))dx=tv=t,
(12)

由於 v=1 對於此問題是常數，因此 (11) 變為

xy^'-y-intsqrt(1+y^('2))dx=0.
(13)

然後微分得到二階常微分方程

xy^('')-sqrt(1+y^('2))=0
(14)

可以解析求解該方程以得到

y=c_1+c_2x^2-(lnx)/(8c_2).
(15)

正如預期的那樣，解涉及兩個任意常數 c_1 和 c_2，其值由初始條件固定。

粒子在時間 t=0 從 (x_0,y_0) 開始的初始條件由下式給出

y(x_0)=y_0
(16)
(dy)/(dx)|_(x_0)=(y_0)/(x_0).
(17)

將這些代入 (15)，求解 c_1 和 c_2，並將結果代回 (15) 得到完整解

y=1/4[(y_0+r_0)eta+(y_0-r_0)lneta+3y_0-r_0],
(18)

其中

eta=(x/(x_0))^2
(19)
r_0=sqrt(x_0^2+y_0^2).
(20)

P 的運動的 y 分量改變方向的點（對應於 y(x) 的最小值，其中 P 轉向並開始從後面跟隨追逐點）可以透過對 (18) 關於 x 求導，將其設定為 0，然後求解 x 來找到。結果是

x^*=x_0sqrt((r_0-y_0)/(r_0+y_0)).
(21)

代入並簡化得到相應的 y 座標，

y^*=(x_0y_0+2r_0y_0-r_0x_0)/(2(r_0+x_0))+1/4(y_0-r_0)ln((r_0-x_0)/(r_0+x_0)).
(22)

也可以用閉合形式表示 x(t) 和 y(t) 的解。將 (◇) 代入 (◇) 並求解 t 得到

t=xy^'-y=1/4[(eta-1)(r_0+y_0)+(r_0-y_0)lneta],
(23)

可以使用 蘭伯特W函式 反轉該式以獲得

x(t)=x_0sqrt((W(chie^(chi-4t/(r_0-y_0))))/chi),
(24)

其中

chi=(r_0+y_0)/(r_0-y_0).
(25)

然後將其代入 y(x) 的方程得到

y(t)=1/4[3y_0-r_0+(y_0-r_0)ln((W(chie^(chi-4t/(r_0-y_0))))/chi)+(y_0+r_0)(W(chie^(chi-4t/(r_0-y_0))))/chi].
(26)
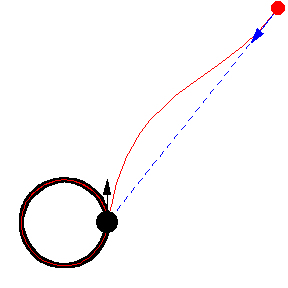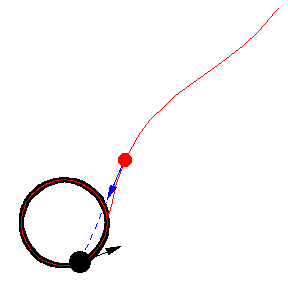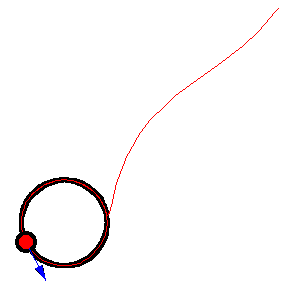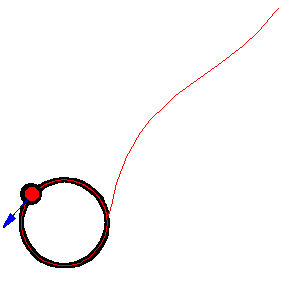
Outside the circle
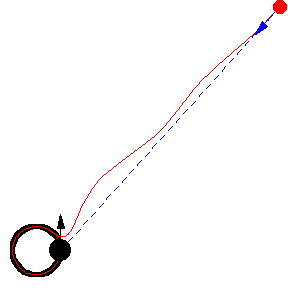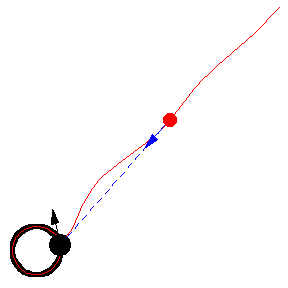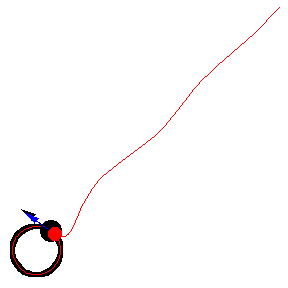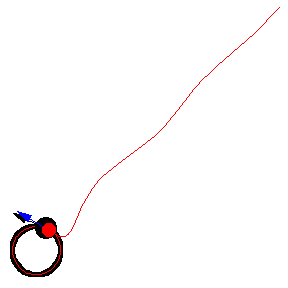
Further outside the circle
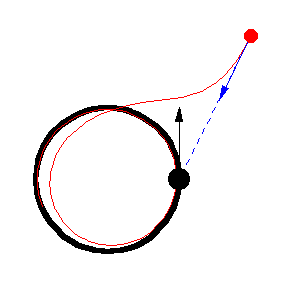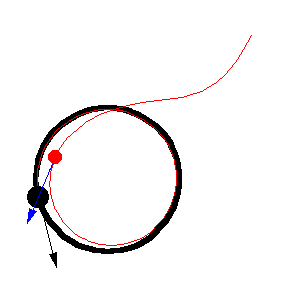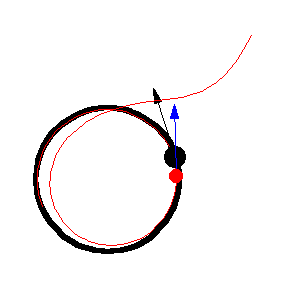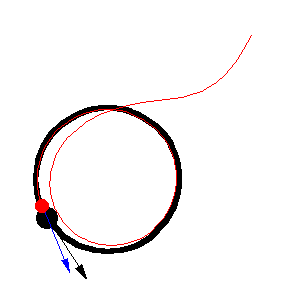
Outside the circle so curve cuts inside
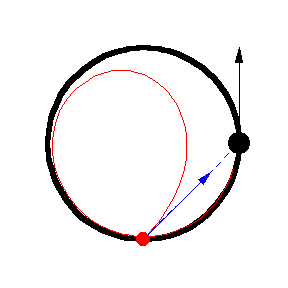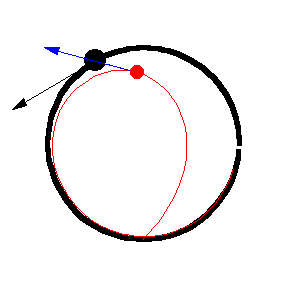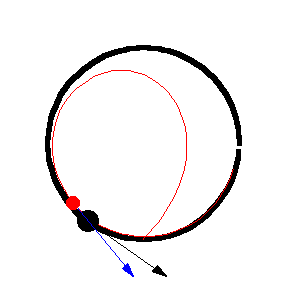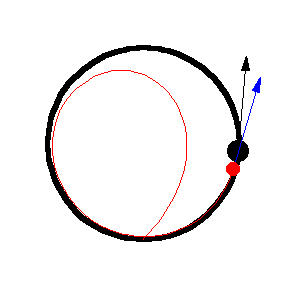
Inside the circle

上圖顯示了 A 以恆定速度繞圓移動的各種追逐曲線。

從正多邊形的角開始並彼此奔跑的 n 只老鼠（或狗）的問題稱為 老鼠問題。

另請參閱

阿波羅尼奧斯追逐問題, 布羅卡爾點, 老鼠問題, 曳物線, 拖網漁船問題, 漩渦線

使用 探索

參考文獻

Barton, J. C. and Eliezer, C. J. "On Pursuit Curves." J. Austral. Math. Soc. Ser. B 41, 358-371, 2000.Bernhart, A. "Curves of Pursuit." Scripta Math. 20, 125-141, 1954.Bernhart, A. "Curves of Pursuit-II." Scripta Math. 23, 49-65, 1957.Bernhart, A. "Polygons of Pursuit." Scripta Math. 24, 23-50, 1959.Bernhart, A. "Curves of General Pursuit." Scripta Math. 24, 189-206, 1959.MacTutor History of Mathematics Archive. "Pursuit Curve." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Pursuit.html.Simmons, G. F. Differential Equations, With Applications and Historical Notes. New York: McGraw-Hill, 1972.Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 327, 1958.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 201-202, 1991.Yates, R. C. "Pursuit Curve." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 170-171, 1952.

在 中被引用

追逐曲線

引用為

Weisstein, Eric W. "追逐曲線。" 來自 ——Wolfram 網路資源。 https://mathworld.tw/PursuitCurve.html

主題分類