主題
Search

三角形重心

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本
Centroid

幾何重心 (質心) 是 多邊形頂點 構成的 三角形 的點 G (有時也表示為 M)，它也是 三角形 三條 三角形中線 的交點 (Johnson 1929, p. 249; Wells 1991, p. 150)。因此，這個點有時被稱為中線點。重心始終位於 三角形 的內部。它具有等價的 三角形中心函式

alpha=1/a
(1)
alpha=bc
(2)
alpha=cscA,
(3)

和齊次 重心座標 (1,1,1)。它是 Kimberling 中心 X_2。

重心滿足

AG^2+BG^2+CG^2=1/3(a^2+b^2+c^2).
(4)

具有三線性頂點 p_i:q_i:r_i，其中 i=1, 2, 3 的三角形的重心由下式給出

(p_1)/(ap_1+bq_1+cr_1)+(p_2)/(ap_2+bq_2+cr_2)+(p_3)/(ap_3+bq_3+cr_3) :(q_1)/(ap_1+bq_1+cr_1)+(q_2)/(aq_2+bq_2+cr_2)+(q_3)/(ap_3+bq_3+cr_3) :(r_1)/(ap_1+bq_1+cr_1)+(r_2)/(ap_2+bq_2+cr_2)+(r_3)/(ap_3+bq_3+cr_3)
(5)

(P. Moses, 私人通訊, Sep. 7, 2005)。

下表總結了作為 Kimberling 中心的命名三角形的三角形重心。

三角形Kimberling三角形重心
反補三角形X_2三角形重心
外法線三角形X_3外心
外切三角形X_3外心
切點三角形X_(354)Weill 點
尤拉三角形X_(381)X_2 和 X_4 的中點
旁心三角形X_(165)旁心三角形的重心
外切圓切點三角形X_(210)X_(10)-Ceva 共軛點 of X_(37)
第一 Brocard 三角形X_2三角形重心
第一 Morley 三角形X_(356)第一 Morley 中心
第一 Neuberg 三角形X_2三角形重心
內心三角形X_(1962)pu(32) 的雙心和
內 Napoleon 三角形X_2三角形重心
內 Vecten 三角形X_2三角形重心
中點三角形X_2三角形重心
垂足三角形X_(51)垂足三角形的重心
外 Napoleon 三角形X_2三角形重心
外 Vecten 三角形X_2三角形重心
參考三角形X_2三角形重心
第二 Neuberg 三角形X_2三角形重心
Stammler 三角形X_3外心
切線三角形X_(154)X_3-Ceva 共軛點 of X_6
CentroidSideRatioCevians

如果 三角形 DeltaA_1A_2A_3 的邊被點 P_1, P_2, 和 P_3 分割，使得

(A_2P_1^_)/(P_1A_3^_)=(A_3P_2^_)/(P_2A_1^_)=(A_1P_3^_)/(P_3A_2^_)=p/q,
(6)

那麼 三角形 DeltaP_1P_2P_3 的重心 G_P 僅僅是 G_A，即原始三角形 DeltaA_1A_2A_3 的重心 (Johnson 1929, p. 250)。

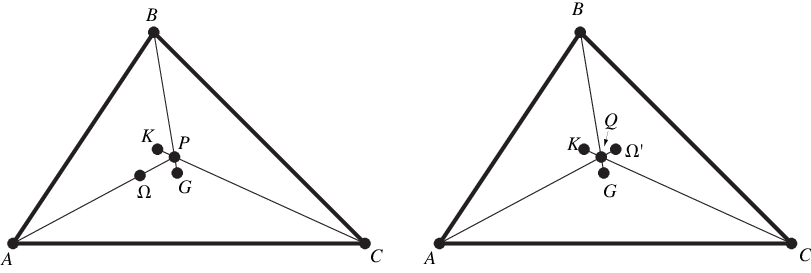
BrocardCentroidLemoine

一條 Brocard 線，一條 三角形中線 和一條 西梅迪安 (每種三條中的一條) 是 共點 的，其中 AOmega，CK 和 BG 交於一點，其中 Omega 是第一 Brocard 點，K 是 西梅迪安點。類似地，AOmega^'，BG 和 CK，其中 Omega^' 是第二 Brocard 點，也交於一點，該點是第一個點的 等角共軛點 (Johnson 1929, pp. 268-269)。

選擇一個內部點 X。三角形 BXC，CXA 和 AXB 具有相等的面積，當且僅當 X 對應於重心時。重心位於每個 多邊形頂點 到對邊 中點 的 2/3 處。每條中線將三角形分成兩個面積相等的部分；所有中線一起將其分成六個相等的部分，並且從重心到 多邊形頂點 的線將整個三角形分成三個等價的 三角形。一般來說，對於 三角形 ABC 平面上的任何直線，

d=1/3(d_A+d_B+d_C),
(7)

其中 d, d_A, d_B, 和 d_C 是從重心和 多邊形頂點 到直線的距離。

三角形 將在重心處以及沿任何穿過重心的直線保持平衡。重心的 三線極線 稱為 Lemoine 軸。從重心出發的 垂線 與 s_i^(-1) 成比例，

a_1p_2=a_2p_2=a_3p_3=2/3Delta,
(8)

其中 Delta 是 三角形 的 面積。設 P 為任意點，多邊形頂點 為 A_1, A_2 和 A_3，重心為 G。那麼

PA_1^2+PA_2^2+PA_3^2=GA_1^2+GA_2^2+GA_3^2+3PG^2.
(9)

如果 O 是三角形重心的 外心，則

OG^2=R^2-1/9(a^2+b^2+c^2).
(10)

到各個命名中心的距離包括

GI=sqrt(-1/(18s)(a^3-2ba^2-2ca^2-2b^2a-2c^2a+9bca+b^3+c^3-2bc^2-2b^2c))
(11)
GH=2/3OH
(12)
GO=1/3OH
(13)
GK=1/(3(a^2+b^2+c^2))(sqrt(-a^6+3b^2a^4+3c^2a^4+3b^4a^2+3c^4a^2-15b^2c^2a^2-b^6-c^6+3b^2c^4+3b^4c^2))
(14)
GL=4/3OH
(15)
GN=1/6OH
(16)
GNa=2IG
(17)
GSp=1/2IG,
(18)

其中 I 是 內心，H 是 垂心，O 是 外心，K 是 西梅迪安點，L 是 de Longchamps 點，N 是 九點中心，Na 是 Nagel 點，以及 Sp 是 Spieker 中心。

重心位於 尤拉線 和 Nagel 線 上。三角形 周長 的重心是三角形的 Spieker 中心 (Johnson 1929, p. 249)。三角形的 西梅迪安點 是其 垂足三角形 的重心 (Honsberger 1995, pp. 72-74)。

MittenpunktCollinear

Gergonne 點 Ge，三角形重心 G 和 Mittenpunkt M 是 共線 的，且 GeG:GM=2:1。

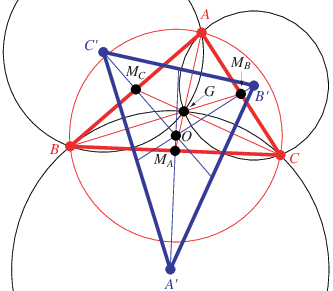
CentroidCircles

給定一個三角形 DeltaABC，構造透過每對頂點且也透過三角形重心 G 的圓。三角形 DeltaA^'B^'C^' 由這些圓的圓心確定，然後滿足許多有趣的性質。第一個是 O 的 外接圓 和三角形重心 G 的 DeltaABC 分別是三角形重心 G^' 和三角形 DeltaA^'B^'C^' 的 西梅迪安點 K^' (Honsberger 1995, p. 77)。此外，DeltaABC 和 DeltaA^'B^'C 的 三角形中線 在 DeltaABC 邊線的中點處 相交。

另請參閱

外心, 尤拉線, 外中點, 內心, Nagel 線, 垂心

在 上探索

參考文獻

Carr, G. S. Formulas and Theorems in Pure Mathematics, 2nd ed. New York: Chelsea, p. 622, 1970.Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., p. 7, 1967.Dixon, R. Mathographics. New York: Dover, pp. 55-57, 1991.Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 72-74 and 77, 1995.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 173-176, 249-250, and 268-269, 1929.Kimberling, C. "Central Points and Central Lines in the Plane of a Triangle." Math. Mag. 67, 163-187, 1994.Kimberling, C. "Centroid." http://faculty.evansville.edu/ck6/tcenters/class/centroid.html.Kimberling, C. "Encyclopedia of Triangle Centers: X(2)=Centroid." http://faculty.evansville.edu/ck6/encyclopedia/ETC.html#X2.Lachlan, R. An Elementary Treatise on Modern Pure Geometry. London: Macmillian, pp. 62-63, 1893.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 150, 1991.

參考內容

三角形重心

引用為

Weisstein, Eric W. "三角形重心。" 來自 Web 資源。 https://mathworld.tw/TriangleCentroid.html

主題分類