主題
Search

幾何質心

質心是二維平面薄片或三維實體的質量中心。具有表面密度函式 sigma(x,y) 的薄片的質量是

M=intintsigma(x,y)dA,
(1)

質心的座標（也稱為重心）是

x^_=(intintxsigma(x,y)dA)/M
(2)
y^_=(intintysigma(x,y)dA)/M.
(3)

薄片的質心是當將其放置在針尖上時能夠保持平衡的點。固體的質心是固體能夠“平衡”的點。

可以使用 Wolfram 語言 計算區域的幾何質心，使用RegionCentroid[reg]。

一組 n 個點質量 m_i 位於位置 x_i 的質心是

x^_=(sum_(i=1)^(n)m_ix_i)/(sum_(i=1)^(n)m_i),
(4)

如果所有質量都相等，則簡化為

x^_=(sum_(i=1)^(n)x_i)/n.
(5)

對於均勻密度的封閉薄片，其邊界由 (x(t),y(t)) 指定，對於 t in [t_0,t_1] 且薄片位於曲線被遍歷時的左側，可以使用 格林定理 計算質心，如下所示

x^_=-1/(2A)int_(t_0)^(t_1)x^2y^'dt
(6)
y^_=1/(2A)int_(t_0)^(t_1)y^2x^'dt.
(7)

平面非自相交多邊形的幾何質心的位置，其頂點為 (x_1,y_1), ..., (x_n,y_n) 是

x^_=1/(6A)sum_(i=1)^(n)(x_i+x_(i+1))(x_iy_(i+1)-x_(i+1)y_i)
(8)
y^_=1/(6A)sum_(i=1)^(n)(y_i+y_(i+1))(x_iy_(i+1)-x_(i+1)y_i),
(9)

其中 A 是多邊形面積，x_(n+1)=x_1 和 y_(n+1)=y_1 (Bourke 1988, Nürnberg 2013)。

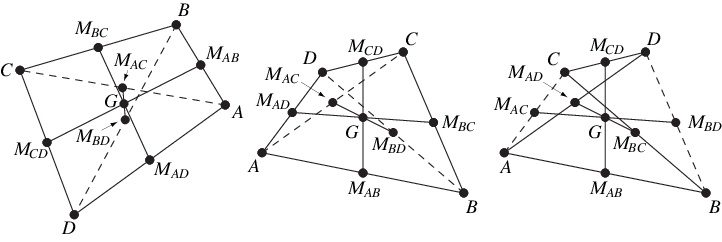
QuadrilateralCentroid

四邊形的頂點質心出現在雙中線的交點處（即，線 M_(AB)M_(CD) 和 M_(AD)M_(BC) 連線相對中點對）（Honsberger 1995, pp. 36-37）。此外，它也是連線對角線 AC 和 BD 中點的線 M_(AC)M_(BD) 的中點（Honsberger 1995, pp. 39-40）。

給定一個任意六邊形，連線每三個連續邊的質心會得到所謂的質心六邊形，這是一個具有相等且平行邊的六邊形（Wells 1991）。

半徑為 R 的半圓的質心由下式給出

x^_=(2R)/pi.
(10)

下表總結了沿非對稱軸的以下曲線所界定的幾個常見薄片的質心。

薄片y^_
扇形(4Rsin(1/2theta))/(3theta)
弓形(4Rsin^3(1/2theta))/(3(theta-sintheta))
等腰三角形1/3h
拋物線弓形2/5h
半圓(4R)/(3pi)

在三維中，密度函式為 rho(x,y,z) 的固體的質量是

M=intintintrho(x,y,z)dV,
(11)

質心的座標是

x^_=(intintintxrho(x,y,z)dV)/M
(12)
y^_=(intintintyrho(x,y,z)dV)/M
(13)
z^_=(intintintzrho(x,y,z)dV)/M.
(14)
固體z^_
圓錐1/4h
圓錐臺(h(R_1^2+2R_1R_2+3R_2^2))/(4(R_1^2+R_1R_2+R_2^2))
半橢球體3/(16)a, 3/(16)b, 3/(16)c
半球體3/8R
拋物面體2/3h
稜錐1/4h
球冠(3(2R-h)^2)/(4(3R-h))
拱頂3/8r

另請參閱

質心六邊形, 質量外心, 帕普斯質心定理, 多邊形質心, 多面體質心

使用 探索

參考文獻

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 132, 1987.Bourke, P. "Calculating the Area and Centroid of a Polygon." July 1988. http://paulbourke.net/geometry/polygonmesh/.Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., 1995.Kern, W. F. and Bland, J. R. "Center of Gravity." §39 in Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 110, 1948.McLean, W. G. and Nelson, E. W. "First Moments and Centroids." Ch. 9 in Schaum's Outline of Theory and Problems of Engineering Mechanics: Statics and Dynamics, 4th ed. New York: McGraw-Hill, pp. 134-162, 1988.Nürnberg, R. "Calculating the Area and Centroid of a Polygon in 2D." 2013. https://www.ma.imperial.ac.uk/~rn/centroid.pdf.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 53-54, 1991.

在 中被引用

幾何質心

請引用本文為

Weisstein, Eric W. "幾何質心。" 來自 Web 資源。 https://mathworld.tw/GeometricCentroid.html

學科分類