主題
Search

施泰納點

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本

存在（至少）三種不同型別的點被稱為施泰納點。

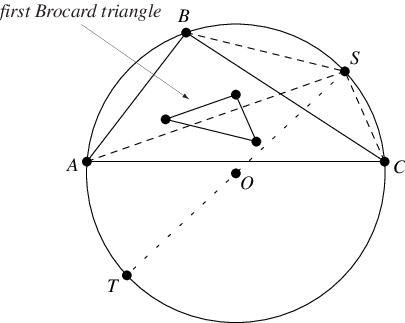
SteinerPoint

透過三角形頂點繪製的三條線，分別平行於第一 布羅卡三角形 的對應邊，這三條線的 交點 S 被稱為施泰納點 (Honsberger 1995)。它位於 外接圓 上，與 塔裡點 T 相對，並具有等價的 三角形中心函式。

alpha=bc(a^2-b^2)(a^2-c^2)
(1)
alpha=1/(a(b^2-c^2)).
(2)

它也位於 施泰納外接橢圓 上。它是 Kimberling 中心 X_(99)。Kiepert 拋物線 的 布里安ション點 也是施泰納點 (Eddy and Fritsch 1994)。類似中線點 K 是第一 布羅卡三角形 的施泰納點 (Honsberger 1995, pp. 120-121)。施泰納點的 西姆森線 平行於 線 OK，其中 O 是 外心，K 是 類似中線點 (Honsberger 1995, p. 121)。

第二種“施泰納點”，更確切地稱為 施泰納曲率質心，是透過在每個頂點放置一個質量等於外角大小的質量而獲得的系統的 幾何質心 (Honsberger 1995, p. 120)。

PascalLines

第三種施泰納點（Steiner 1827-1828；Lachlan 1893，pp. 115-116）產生於 帕斯卡定理 中 圓錐曲線 上的相對邊三元組在 頂點 的所有排列中延伸時，產生 60 條 帕斯卡線。它們三條線的交點，共有 20 個點，被稱為施泰納點。施泰納定理 指出，這些點是由六邊形 123456、143652 和 163254 生成的，這些六邊形是透過交換位置 2、4 和 6 處的頂點形成的（其中數字表示六邊形頂點的選取順序）。上面顯示了內接於一般橢圓的一般六邊形的 帕斯卡線 的配置，其中施泰納點顯示為填充圓圈。下面顯示了左上角圖形區域的放大圖，說明了每條施泰納點處三條帕斯卡線的共點。

SteinerPoints

每個施泰納點與三個 柯克曼點 一起位於總共 20 條稱為 凱萊線 的線上。施泰納點也一次四個地位於 15 條 普呂克線 上 (Wells 1991)。20 個施泰納點和 20 條 凱萊線 之間存在對偶關係。

另請參閱

布里安ション點, 布羅卡三角形, 凱萊線, 外接圓, 圓錐曲線, Kiepert 拋物線, 柯克曼點, 類似中線點, 帕斯卡線, 帕斯卡定理, 普呂克線, Salmon 點, 施泰納曲率質心, 施泰納集, 施泰納定理, 施泰納三元系, 塔裡點

使用 探索

參考文獻

Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 66 and 329, 1893.Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, p. 77, 1971.Eddy, R. H. and Fritsch, R. "The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle." Math. Mag. 67, 188-205, 1994.Gallatly, W. "The Steiner and Tarry Points." §143 in The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 102, 1913.Honsberger, R. "The Steiner Point and the Tarry Point." §10.5 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 119-124, 1995.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 236-237, 281-282, 1929.Kimberling, C. "Central Points and Central Lines in the Plane of a Triangle." Math. Mag. 67, 163-187, 1994.Kimberling, C. "Steiner Point." http://faculty.evansville.edu/ck6/tcenters/class/steiner.html.Kimberling, C. "Encyclopedia of Triangle Centers: X(99)=Steiner Point." http://faculty.evansville.edu/ck6/encyclopedia/ETC.html#X99.Lachlan, R. An Elementary Treatise on Modern Pure Geometry. London: Macmillian, 1893.Neuberg, J. "Sur le point de Steiner." J. de math. spéciales, p. 29, 1886.Salmon, G. "Notes: Pascal's Theorem, Art. 267" in A Treatise on Conic Sections, 6th ed. New York: Chelsea, pp. 379-382, 1960.Steiner, J. "Questions proposées. Théorèmes sur l'hexagramum mysticum." Ann. Math. 18, 339-340, 1827-1828.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 172, 1991.

在 上引用

施泰納點

引用為

Weisstein, Eric W. “施泰納點。” 來自 Web 資源。 https://mathworld.tw/SteinerPoints.html

主題分類