雙曲正弦定義為
 |
(1)
|
符號  有時也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 語言 中被實現為Sinh[z].
有時也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 語言 中被實現為Sinh[z].
特殊值包括
其中  是 黃金比例。
是 黃金比例。
值
 |
(4)
|
(OEIS A073742) 具有 Engel 展開式 1, 6, 20, 42, 72, 110, ... (OEIS A068377),其閉合形式為  對於
對於  。
。
導數 由下式給出
 |
(5)
|
其中  是 雙曲餘弦,不定積分 由下式給出
是 雙曲餘弦,不定積分 由下式給出
 |
(6)
|
其中  是 積分常數。
是 積分常數。
 具有 泰勒級數
具有 泰勒級數
(OEIS A009445)。
另請參閱
Beta 指數函式,
雙極座標,
雙極柱座標,
雙球座標,
懸鏈線,
懸鏈面,
圓錐函式,
三次方程,
棣莫弗恆等式,
Dixon-Ferrar 公式,
橢圓柱座標,
Elsasser 函式,
古德曼函式,
螺旋麵,
亥姆霍茲微分方程——橢圓柱座標,
雙曲餘割,
雙曲函式,
反雙曲正弦,
拉普拉斯方程——雙球座標,
拉普拉斯方程——環面座標,
Lebesgue 常數,
洛倫茲群,
墨卡託投影,
米勒圓柱投影,
第二類修正貝塞爾函式,
第一類修正球貝塞爾函式,
修正斯特魯夫函式,
Nicholson 公式,
扁球面座標,
拋物線漸屈線,
分割函式 P,
Poinsot 螺線,
長球面座標,
Schläfli 公式,
Shi,
正弦,
Sine-Gordon 方程,
旋轉曲面,
Tau 函式,
環面座標,
環面函式,
曳物線,
Watson 公式
使用 探索
參考文獻
Abramowitz, M. 和 Stegun, I. A. (編輯)。 "雙曲函式。" §4.5 在 數學函式手冊,包含公式、圖表和數學表格,第 9 版。 紐約:Dover,pp. 83-86, 1972。Gradshteyn, I. S. 和 Ryzhik, I. M. 積分表、級數和乘積表,第 6 版。 聖地亞哥,加利福尼亞州:Academic Press,2000。Jeffrey, A. "雙曲恆等式。" §2.5 在 數學公式和積分手冊,第 2 版。 奧蘭多,佛羅里達州:Academic Press,pp. 117-122, 2000。Sloane, N. J. A. 整數序列 A009445, A068377, 和 A073742 在 "整數序列線上百科全書" 中。Spanier, J. 和 Oldham, K. B. "雙曲正弦  和餘弦
和餘弦  函式。" 第 28 章 在 函式圖集。 華盛頓特區:Hemisphere,pp. 263-271, 1987。Zwillinger, D. (編輯)。 "雙曲函式。" §6.7 在 CRC 標準數學表格和公式。 博卡拉頓,佛羅里達州:CRC Press,pp. 476-481 1995。
函式。" 第 28 章 在 函式圖集。 華盛頓特區:Hemisphere,pp. 263-271, 1987。Zwillinger, D. (編輯)。 "雙曲函式。" §6.7 在 CRC 標準數學表格和公式。 博卡拉頓,佛羅里達州:CRC Press,pp. 476-481 1995。在 上被引用
雙曲正弦
引用為
Weisstein, Eric W. "雙曲正弦。" 來自 —— 資源。 https://mathworld.tw/HyperbolicSine.html
主題分類
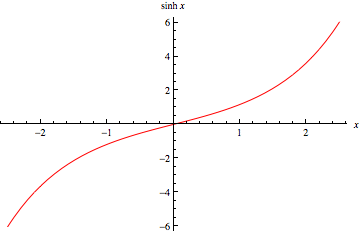
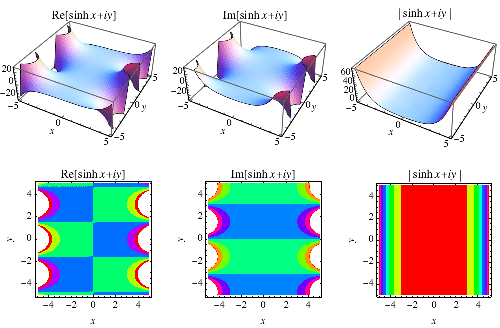
有時也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 語言 中被實現為Sinh[z].
是 黃金比例。
對於
。
是 積分常數。
具有 泰勒級數
