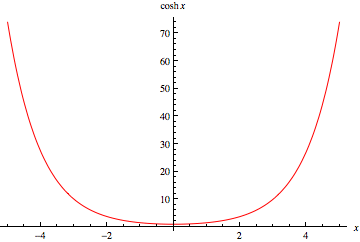
雙曲餘弦定義為
 |
(1)
|
有時也使用符號  (Gradshteyn and Ryzhik 2000, p. xxix)。此函式描述了懸鏈線的形狀,稱為 懸鏈線。它在 Wolfram 語言 中實現為Cosh[z].
(Gradshteyn and Ryzhik 2000, p. xxix)。此函式描述了懸鏈線的形狀,稱為 懸鏈線。它在 Wolfram 語言 中實現為Cosh[z].
特殊值包括
其中  是黃金比例。
是黃金比例。
導數由下式給出
 |
(4)
|
其中  是雙曲正弦,不定積分由下式給出
是雙曲正弦,不定積分由下式給出
 |
(5)
|
其中  是積分常數。
是積分常數。
雙曲餘弦的泰勒級數為
(OEIS A010050)。
另請參閱
雙極座標,
雙極柱座標,
雙球面座標,
懸鏈線,
懸鏈面,
Chi,
圓錐函式,
相關係數--雙變數正態分佈,
餘弦,
三次方程,
棣莫弗恆等式,
橢圓柱座標,
埃爾薩瑟函式,
雙曲函式,
雙曲幾何,
雙曲蘭氏曲線函式,
雙曲正弦,
雙曲正割,
雙曲正切,
反演距離,
反雙曲餘弦,
拉普拉斯方程--雙極座標,
拉普拉斯方程--雙球面座標,
拉普拉斯方程--環面座標,
蘭氏曲線函式,
洛倫茲群,
馬蒂厄微分方程,
梅勒的貝塞爾函式公式,
墨卡託投影,
第一類修正貝塞爾函式,
扁球面座標,
長球面座標,
偽球面,
拉馬努金 Cos/Cosh 恆等式,
正弦-戈爾登方程,
旋轉曲面,
環面座標
使用 探索
參考文獻
Abramowitz, M. and Stegun, I. A. (編). "Hyperbolic Functions." §4.5 在Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 頁 83-86, 1972.Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.Jeffrey, A. "Hyperbolic Identities." §2.5 在 Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, 頁 117-122, 2000.Sloane, N. J. A. 序列 A010050 在 "整數序列線上百科全書"。Spanier, J. and Oldham, K. B. "The Hyperbolic Sine  and Cosine
and Cosine  函式。" 章 28 在 An Atlas of Functions. Washington, DC: Hemisphere, 頁 263-271, 1987.Zwillinger, D. (編). "Hyperbolic Functions." §6.7 在 CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 頁 476-481 1995.
函式。" 章 28 在 An Atlas of Functions. Washington, DC: Hemisphere, 頁 263-271, 1987.Zwillinger, D. (編). "Hyperbolic Functions." §6.7 在 CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 頁 476-481 1995.在 上被引用
雙曲餘弦
引用為
Weisstein, Eric W. "Hyperbolic Cosine." 來自 Web 資源。 https://mathworld.tw/HyperbolicCosine.html
主題分類
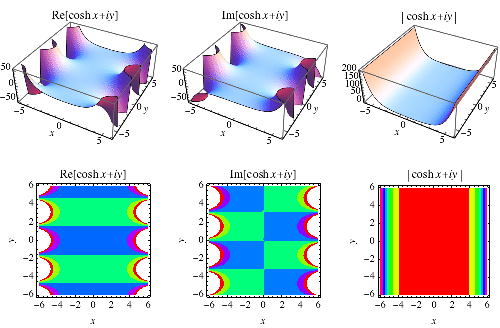
(Gradshteyn and Ryzhik 2000, p. xxix)。此函式描述了懸鏈線的形狀,稱為 懸鏈線。它在 Wolfram 語言 中實現為Cosh[z].
是黃金比例。
是雙曲正弦,不定積分由下式給出
是積分常數。
