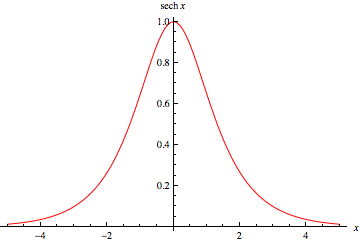
雙曲正割定義為
其中  是雙曲餘弦。它在 Wolfram 語言 中被實現為Sech[z]。
是雙曲餘弦。它在 Wolfram 語言 中被實現為Sech[z]。
在實數線上,它在  處有最大值,拐點在
處有最大值,拐點在  (OEIS A091648)。它在
(OEIS A091648)。它在  處有一個不動點 (OEIS A069814)。
處有一個不動點 (OEIS A069814)。
導數由下式給出
 |
(3)
|
其中  是雙曲正切,不定積分由下式給出
是雙曲正切,不定積分由下式給出
![intsechzdz=2tan^(-1)[tanh(1/2z)]+C,](/images/equations/HyperbolicSecant/NumberedEquation2.svg) |
(4)
|
其中  是積分常數。
是積分常數。
 具有泰勒級數
具有泰勒級數
(OEIS A046976 和 A046977),其中  是尤拉數,
是尤拉數, 是階乘。
是階乘。
在拉馬努金 cos/cosh 恆等式中,將  ,
,  , 和
, 和  的係數相等
的係數相等
![[1+2sum_(n=1)^infty(cos(ntheta))/(cosh(npi))]^(-2)+[1+2sum_(n=1)^infty(cosh(ntheta))/(cosh(npi))]^(-2)=(2Gamma^4(3/4))/pi](/images/equations/HyperbolicSecant/NumberedEquation3.svg) |
(7)
|
給出驚人的恆等式
![sum_(n=1)^inftysech(pin)=1/2{(sqrt(pi))/([Gamma(3/4)]^2)-1}
sum_(n=1)^inftyn^4sech(pin)=(18[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]^2
sum_(n=1)^inftyn^8sech(pin)=(168[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]×sum_(n=1)^inftyn^6sech(pin)-(63000[Gamma(3/4)]^6)/(pi^(3/2))[sum_(n=1)^inftyn^2sech(pin)]^4.](/images/equations/HyperbolicSecant/NumberedEquation4.svg) |
(8)
|
另請參閱
Benson 公式,
懸鏈線,
懸鏈面,
尤拉數,
高斯函式,
雙曲餘弦,
雙曲函式,
反雙曲正割,
洛倫茲函式,
扁球面座標,
偽球面,
正割,
旋轉曲面,
曳物線,
阿涅西的女巫曲線
使用 探索
參考文獻
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.Sloane, N. J. A. Sequences A046976, A046977, A069814, and A091648 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "The Hyperbolic Secant  and Cosecant
and Cosecant  Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.
Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.在 上被引用
雙曲正割
請引用為
Weisstein, Eric W. “雙曲正割。” 來自 Web 資源。 https://mathworld.tw/HyperbolicSecant.html
主題分類
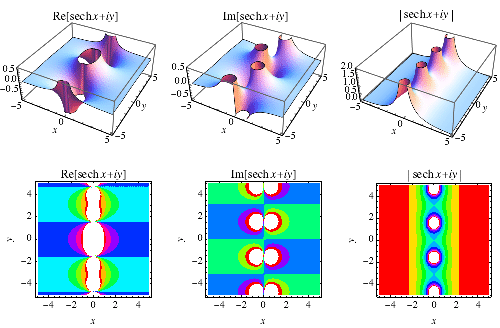
是雙曲餘弦。它在 Wolfram 語言 中被實現為Sech[z]。
處有最大值,拐點在
(OEIS A091648)。它在
處有一個不動點 (OEIS A069814)。
是積分常數。
具有泰勒級數
是尤拉數,
是階乘。
,
, 和
的係數相等
![[1+2sum_(n=1)^infty(cos(ntheta))/(cosh(npi))]^(-2)+[1+2sum_(n=1)^infty(cosh(ntheta))/(cosh(npi))]^(-2)=(2Gamma^4(3/4))/pi](/images/equations/HyperbolicSecant/NumberedEquation3.svg)
![sum_(n=1)^inftysech(pin)=1/2{(sqrt(pi))/([Gamma(3/4)]^2)-1}
sum_(n=1)^inftyn^4sech(pin)=(18[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]^2
sum_(n=1)^inftyn^8sech(pin)=(168[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]×sum_(n=1)^inftyn^6sech(pin)-(63000[Gamma(3/4)]^6)/(pi^(3/2))[sum_(n=1)^inftyn^2sech(pin)]^4.](/images/equations/HyperbolicSecant/NumberedEquation4.svg)