主題
Search

高斯函式

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
GaussianReal
最小值 最大值
Powered by webMathematica
GaussianReImAbs
最小值 最大值
實部
虛部 Powered by webMathematica

在一維中，高斯函式是 機率密度函式 的 正態分佈，

f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)),
(1)

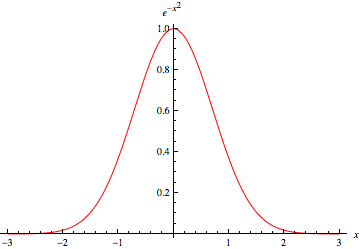
有時也稱為 頻率曲線。 半峰全寬 (FWHM) 是透過找到半最大值點 x_0 找到的。 常數比例因子可以忽略，所以我們必須求解

e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max))
(2)

但 f(x_(max)) 發生在 x_(max)=mu，所以

e^(-(x_0-mu)^2/(2sigma^2))=1/2f(mu)=1/2.
(3)

求解，

e^(-(x_0-mu)^2/(2sigma^2))=2^(-1)
(4)
-((x_0-mu)^2)/(2sigma^2)=-ln2
(5)
(x_0-mu)^2=2sigma^2ln2
(6)
x_0=+/-sigmasqrt(2ln2)+mu.
(7)

因此，半峰全寬 由下式給出

FWHM=x_+-x_-=2sqrt(2ln2)sigma approx 2.3548sigma.
(8)
GaussianFunction2D

在二維中，圓形高斯函式是不相關變數 X 和 Y 的分佈函式，這些變數具有 二元正態分佈 和相等的 標準差 sigma=sigma_x=sigma_y，

f(x,y)=1/(2pisigma^2)e^(-[(x-mu_x)^2+(y-mu_y)^2]/(2sigma^2)).
(9)

相應的橢圓高斯函式對應於 sigma_x!=sigma_y，由下式給出

f(x,y)=1/(2pisigma_xsigma_y)e^(-[(x-mu_x)^2/(2sigma_x^2)+(y-mu_y)^2/(2sigma_y^2)]).
(10)
GaussianApodization

高斯函式也可以用作 切趾函式

A(x)=e^(-x^2/(2sigma^2)),
(11)

如上所示，帶有相應的 儀器函式。儀器函式是

I(k)=e^(-2pi^2k^2sigma^2)sigmasqrt(pi/2)[erf((a-2piiksigma^2)/(sigmasqrt(2)))+erf((a+2piiksigma^2)/(sigmasqrt(2)))],
(12)

其最大值為

I_(max)=sigmasqrt(2pi)erf(a/(sigmasqrt(2))).
(13)

當 a->infty 時，方程 (12) 簡化為

lim_(a->infty)I(k)=sigmasqrt(2pi)e^(-2pi^2k^2sigma^2).
(14)

超幾何函式有時也稱為高斯函式。

另請參閱

二元正態分佈, Erf, Erfc, 傅立葉變換--高斯, 雙曲正割, 洛倫茲函式, 正態分佈, Owen T 函式, 阿涅西的女巫曲線

使用 探索

參考文獻

MacTutor History of Mathematics Archive. "頻率曲線。" http://www-groups.dcs.st-and.ac.uk/~history/Curves/Frequency.html。

在 上被引用

高斯函式

請引用為

Weisstein, Eric W. "高斯函式。" 來自 Web 資源。 https://mathworld.tw/GaussianFunction.html

主題分類