洛倫茲函式

最小值 最大值

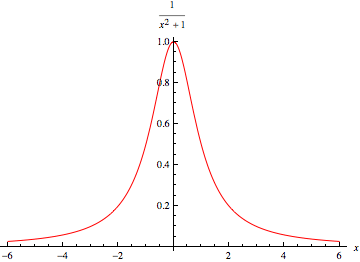
洛倫茲函式是由以下單峰函式給出：

其中 是中心， 是指定寬度的引數。 洛倫茲函式被歸一化，使得

它在 處有最大值，其中

它在最大值處的值是

它在

處等於其最大值的一半，因此具有半峰全寬 。 該函式在

處有拐點，給出

其中

最小值 最大值 實部 虛部

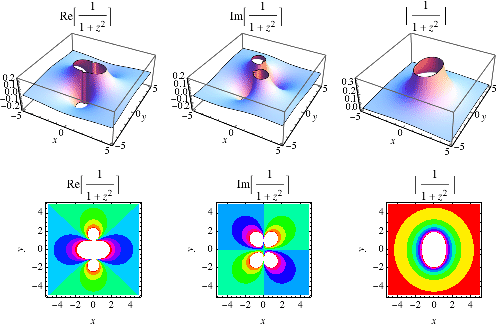擴充套件到複平面的洛倫茲函式如上圖所示。

洛倫茲函式給出了某些型別譜線的形狀，並且是柯西分佈中的分佈函式。 洛倫茲函式具有傅立葉變換

洛倫茲函式也可以用作孔徑函式，儘管其儀器函式在解析上難以表達。