“阿涅西的女巫曲線”是由瑪麗亞·阿涅西於 1748 年在她的著作《Instituzioni analitiche ad uso della gioventù italiana 》(第一部由女性撰寫的現存數學著作)中研究的曲線。這條曲線也被稱為阿涅西三次曲線或阿涅西曲線,並且早先在 1703 年已被費馬和圭多·格蘭迪研究過。
“女巫”這個名字源於對原始著作中術語 averisera (“正矢曲線”,來自拉丁語 vertere ,“轉動”)的誤譯,在 1801 年劍橋盧卡斯數學教授約翰·科爾森 (Gray) 對該著作的翻譯中,被誤譯為 avversiera (“女巫”或“魔鬼的妻子”)。
該曲線是透過從原點繪製一條線
引數形式為,
對於
對於
笛卡爾方程可以透過在引數方程中消去
(5)
這在函式形式上等價於洛倫茲函式 。
曲線與
(6)
該曲線在 拐點 。直線 漸近線 。
第二種引數化中的曲率 和切線角 由下式給出
另請參閱 高斯函式 ,
雙曲正割 ,
拉梅曲線 ,
洛倫茲函式
使用 探索
參考文獻 Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Gray, S. "History of the Name 'Witch.' " http://instructional1.calstatela.edu/sgray/Agnesi/WitchHistory/Historynamewitch.html . Lawrence, J. D. A Catalog of Special Plane Curves. MacTutor History of Mathematics Archive. "Witch of Agnesi." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Witch.html . Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. Yates, R. C. "Witch of Agnesi." A Handbook on Curves and Their Properties.
請引用為
韋斯坦因,埃裡克·W. "阿涅西的女巫曲線。" 來自 https://mathworld.tw/WitchofAgnesi.html
主題分類
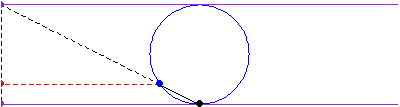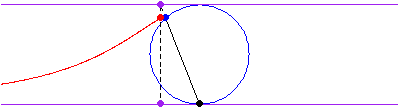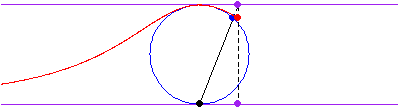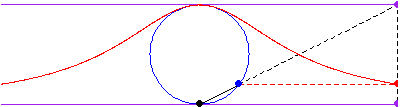
,穿過半徑為
,中心為
的圓而獲得的,然後選取與圓的交點的
座標,以及線
的延長線與直線
的交點的
座標來確定曲線上的點。
, 或
.
得到,為
軸之間的面積為

![-tan^(-1)[(2t)/((1+t^2)^2)].](/images/equations/WitchofAgnesi/Inline31.svg)