主題
Search

反雙曲正割

下載 Mathematica Notebook下載 Wolfram Notebook
ArcSech
ArcSechReImAbs
最小值 最大值
實部
虛部 Powered by webMathematica

反雙曲正割 sech^(-1)z (Beyer 1987, p. 181; Zwillinger 1995, p. 481)，有時稱為面積雙曲正割 (Harris and Stocker 1998, p. 271)，有時也記作 arcsechz (Jeffrey 2000, p. 124)，是 多值函式，它是 反函式，也是 雙曲正割 的反函式。變體 Arcsechz 或 Arsechz (Harris and Stocker 1998, p. 263) 有時用於指代反雙曲正割的顯式 主值，儘管這種區分並不總是明確的。更糟糕的是，符號 arccschz 有時用於主值，而 Arcsechz 用於多值函式 (Abramowitz and Stegun 1972, p. 87)。請注意，在符號 sech^(-1)z 中，sechz 是 雙曲正割，而上標 -1 表示 反函式，不是 乘法逆元。

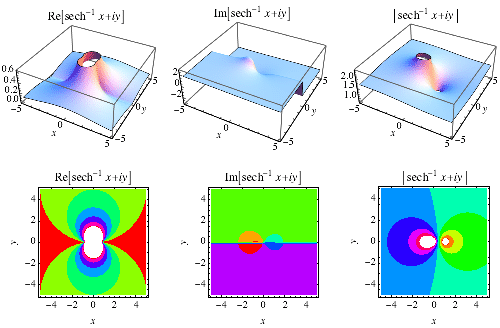
主值 的 sech^(-1)z 在 Wolfram 語言 中實現為ArcSech[z].

InverseHyperbolicSecantBranchCut

反雙曲正割是一個 多值函式，因此需要在 複平面 中 支割線，Wolfram 語言 的約定將其放置線上段 (-infty,0] 和 (1,infty) 處。這源於 sech^(-1)z 的定義，即

sech^(-1)z=ln(sqrt(1/z-1)sqrt(1/z+1)+1/z).
(1)

對於實數 x，它滿足

sech^(-1)x={ln((1-sqrt(1-x^2))/x) for x<-1; ln((1+sqrt(1-x^2))/x) for x>0.
(2)

反雙曲正割的 導數 由下式給出

d/zsech^(-1)z=-1/(z(z+1)sqrt((1-z)/(1+z))),
(3)

及其 不定積分 為

intsech^(-1)zdz =zsech^(-1)z-tan^(-1)(z/(z-1)sqrt((1-z)/(1+z)))+C.
(4)

它有 麥克勞林級數

sech^(-1)x=-lnx+ln2+sum_(n=1)^(infty)((-1)^(n+1)(2n-1)!!)/(2n(2n)!!)x^(2n)
(5)
=-lnx+ln2-1/4x^2-3/(32)x^4-5/(96)x^6-(35)/(1024)x^8+...
(6)

(OEIS A052468 和 A052469)。

另請參閱

雙曲正割, 反雙曲函式

相關 Wolfram 網站

http://functions.wolfram.com/ElementaryFunctions/ArcSech/

使用 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in 數學函式手冊，包含公式、圖表和數學表格，第 9 次印刷。 New York: Dover, pp. 79-83, 1972.Beyer, W. H. CRC 標準數學表格，第 28 版。 Boca Raton, FL: CRC Press, pp. 142-143, 1987.Harris, J. W. 和 Stocker, H. 數學與計算科學手冊。 New York: Springer-Verlag, 1998.Jeffrey, A. 數學公式與積分手冊，第 2 版。 Orlando, FL: Academic Press, 2000.Sloane, N. J. A. 序列 A052468 和 A052469 在“整數序列線上百科全書”中。Spanier, J. 和 Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in 函式圖集。 Washington, DC: Hemisphere, pp. 331-341, 1987.Zwillinger, D. (Ed.). CRC 標準數學表格與公式。 Boca Raton, FL: CRC Press, 1995.

在 中被引用

反雙曲正割

請引用為

Weisstein, Eric W. “反雙曲正割。” 來自 —— 資源。 https://mathworld.tw/InverseHyperbolicSecant.html

學科分類