古德曼函式

最小值 最大值

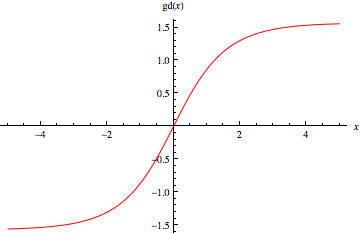
古德曼函式是一個奇函式，用 或 表示，它出現在墨卡託投影的反方程中。 表示緯度 用垂直位置 在此投影中表示，因此古德曼函式定義為

對於實數 ，此定義也等於

古德曼函式在 Wolfram 語言 中實現為古德曼函式[z].

古德曼函式的導數為

其不定積分為

其中 是雙對數函式。

它具有麥克勞林級數

(OEIS A091912 和 A136606)。

古德曼函式透過以下方式連線了三角函式和雙曲函式

古德曼函式透過以下方式與指數函式相關

(Beyer 1987, p. 164; Zwillinger 1995, p. 485)。

其他基本恆等式為

(Zwillinger 1995, p. 485)。

如果 ，那麼

(Beyer 1987, p. 164; Zwillinger 1995, p. 530)，其中最後一個恆等式已被更正。

另一個恆等式由下式給出

(M. Somos, 私人通訊，2006 年 4 月 15 日)。

最小值 最大值 實部 虛部

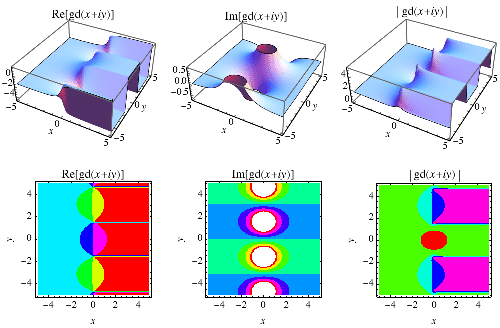古德曼函式也可以擴充套件到複平面，如上圖所示。