凱萊圖

設 為一個 群，並設 為群元素的集合，使得 單位元 。與 關聯的凱萊圖被定義為 有向圖，其頂點與每個群元素關聯，且有有向邊 ，每當 時。凱萊圖可能取決於生成集的選擇，並且是 連通的 當且僅當 生成 （即，集合 是 的 群生成元）。

需要注意的是，術語“凱萊圖”也用於 被隱式地理解為群的生成元集合時，在這種情況下，圖總是連通的（但通常，仍然取決於生成元的選擇）。群 的這種凱萊圖可以使用 Wolfram 語言 計算，使用CayleyGraph[G]，其中使用的生成元是那些由以下命令返回的生成元GroupGenerators[G]。

更復雜的是，適當有向凱萊圖的無向版本也被稱為凱萊圖。

特定生成元集合的 交錯群 的無向凱萊圖有時被稱為 交錯群圖。迴圈群 的凱萊圖是 圈圖 ，而 二面體群 的凱萊圖是 稜柱圖 。其他屬於凱萊圖的圖類包括 迴圈圖（如果需要生成集則連通；如果不要求則可能不連通）、立方體連線環、漢明圖 和 超立方體圖。

有向圖凱萊圖的每個節點的 邊重數 相同。（有向或無向）凱萊圖始終是 頂點傳遞圖，但反之不一定成立。然而，在小型 頂點傳遞圖 中，很大一部分是凱萊圖（McKay 和 Royle 1990）。

Royle 維護了一個非必要連通的頂點傳遞圖列表，其中包含頂點數最多為 31 的凱萊圖或非凱萊圖的指定，儘管對於 27、28 和 30 個頂點的值尚未經過獨立驗證（儘管群中的錯誤只會影響圖，如果以某種方式遺漏了最小傳遞群，因此不太可能出現錯誤）。頂點數為 , 2, ... 的非必要連通凱萊圖的數量分別為 1, 2, 2, 4, 3, 8, 4, 14, 9, 20, 8, 74, ... （OEIS A185959；McKay 和 Royle 1990，McKay 和 Praeger 1994），以及存在非凱萊頂點傳遞圖的頂點數分別為 10, 15, 16, 18, 20, 24, 26, 28, 30, ....

最小的頂點傳遞非凱萊圖是 彼得森圖 （McKay 和 Praeger 1994），而最小的非連通頂點傳遞非凱萊圖是兩個 的副本。

凱萊圖可以透過從生成元排列集合 （不包括單位排列）開始生成，並相互排列元素直到不再有新的排列產生。這會產生一個在元素排列下閉合的集合 。如果對於某些 ， 成立，則連線每對排列 與一條邊，然後得到一個凱萊圖。

唯一可以給出平面凱萊圖的群恰好是 、、、、 和 ，正如 Maschke (1896) 所證明的那樣。

下表列出了一些由少量小排列生成的凱萊圖的無向版本。

圖	生成元
16-胞 圖	1,2,4,3, 2,1,3,4, 2,1,4,3, 3,4,1,2, 3,4,2,1
迴圈圖	1,2,3,5,4, 1,2,4,3,5, 2,1,3,5,4, 2,1,5,4,3
完全二分圖	1,2,4,3, 2,1,3,4, 3,4,2,1
	1,2,4,3, 2,1,3,4, 3,4,1,2, 4,3,2,1
	1,2,4,5,6,3, 2,1,4,5,6,3
完全圖	1,3,2, 2,1,3, 2,3,1, 3,2,1
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,3,2
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,2,3, 1,4,3,2
立方圖	1,2,4,3, 3,4,2,1
	1,2,4,3, 2,1,3,4, 3,4,1,2
	1,2,3,5,4, 1,4,5,3,2
立方對稱圖	1,2,4,3, 1,3,2,4, 3,2,1,4
	1,2,3,4,6,5, 2,5,4,6,3,1
立方對稱圖	1,3,2,5,4, 2,1,4,3,5, 4,5,3,1,2
立方頂點傳遞圖 Ct19	1,2,3,4,6,5, 1,2,4,3,6,5, 5,6,3,4,1,2
立方頂點傳遞圖 Ct23	1,2,3,4,6,5, 2,3,1,5,6,4
立方頂點傳遞圖 Ct28	1,3,2,5,4, 2,3,4,1,5
立方頂點傳遞圖 Ct37	1,2,4,3, 1,3,2,4,3,4,1,2
立方頂點傳遞圖 Ct38	1,2,3,4,5,7,6, 2,3,1,6,7,4,5
立方頂點傳遞圖 Ct41	1,2,4,3, 1,3,2,4,2,1,4,3
立方頂點傳遞圖 Ct42	1,2,3,4,5,7,6, 2,3,4,1,6,5,7
立方八面體圖	1,3,4,2, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,3,1,4, 3,1,2,4
	1,2,4,5,3, 1,3,4,2,5
5-圈圖	2,3,4,5,1, 5,1,2,3,4
6-圈圖	1,3,2, 2,1,3
	1,2,4,3, 1,3,2,4
	1,2,3,5,4, 1,2,4,3,5
8-圈圖	1,2,4,3, 3,4,1,2
	1,2,3,5,4, 1,4,5,2,3
10-圈圖	1,3,2,5,4, 2,1,4,3,5
12-圈圖	1,2,3,5,4, 2,1,4,3,5
富蘭克林圖	1,2,3,5,4, 1,2,4,3,5, 2,1,3,5,4
	1,2,3,4,5,7,6, 1,2,3,4,6,5,7, 1,2,4,3,5,7,6
大斜方立方八面體圖	1,2,3,4,5,7,6, 1,2,3,4,6,5,7, 1,3,2,5,4,7,6
二十面體圖	1,3,4,2, 2,1,4,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,1,4,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,1,4,3, 2,3,1,4, 3,1,2,4
4-莫比烏斯梯子	1,2,4,3, 2,1,4,3, 3,4,1,2
八面體圖	1,3,2, 2,1,3, 2,3,1
	1,2,4,3, 1,3,2,4, 1,3,4,2
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,2,3
	1,2,4,5,3, 2,1,4,5,3
	1,2,4,5,3, 2,1,4,5,3
帕普斯圖	1,2,3,4,6,5, 2,3,1,5,4,6
2-路徑圖	2,1
	1,3,2
五胞體 圖	2,3,4,5,1, 3,4,5,1,2
5-稜柱圖	1,3,2,5,4, 2,4,1,5,3
	1,3,2,5,4, 2,4,1,5,3
6-稜柱圖	1,2,3,5,4, 2,1,4,5,3
	1,2,3,5,4, 2,1,4,5,3
小斜方二十面十二面體圖	1,2,4,5,3, 3,4,2,5,1
小斜方立方八面體圖	1,3,4,2, 2,3,4,1
	1,3,4,2, 1,4,2,3, 2,3,4,1
	1,3,4,2, 1,4,2,3, 2,3,4,1, 4,1,2,3
	1,2,4,5,3, 1,3,4,5,2
扭稜立方圖	1,2,4,3, 2,3,1,4, 2,3,4,1
	1,2,4,3, 2,3,1,4, 2,3,4,1, 3,1,2,4
	1,2,4,3, 2,3,1,4, 2,3,4,1, 3,1,2,4, 4,1,2,3
正方形 反稜柱圖	1,2,4,3, 3,4,1,2, 3,4,2,1
	1,2,4,3, 3,4,1,2, 3,4,2,1, 4,3,1,2
正方圖	1,2,4,3, 2,1,3,4
	1,2,3,5,4, 1,3,2,4,5
超立方體圖	1,2,3,4,6,5, 1,2,4,3,5,6, 3,4,2,1,5,6
四面體圖	2,1,4,3, 3,4,2,1
	1,2,4,3, 2,1,3,4, 2,1,4,3
	1,3,2,5,4, 1,4,5,3,2
三角形圖	2,3,1
	1,3,4,2, 1,4,2,3
	1,2,4,5,3, 1,2,5,3,4
三角 稜柱圖	1,3,2, 2,3,1
	1,2,4,3, 1,3,4,2
	1,2,4,3, 1,3,4,2, 1,4,2,3
	1,2,3,5,4, 1,2,4,5,3
截角立方體圖	1,2,4,3, 2,3,1,4
	1,2,4,3, 2,3,1,4, 3,1,2,4
	1,2,3,5,4, 1,3,4,2,5
截角十二面體圖	1,2,4,5,3, 3,4,1,2,5
截角二十面體圖	1,3,2,5,4, 2,3,4,5,1
截角八面體圖	1,2,4,3, 2,3,4,1
	1,2,4,3, 1,3,2,4, 2,1,3,4
	1,2,3,5,4, 1,3,4,5,2
截角四面體圖	1,3,4,2, 2,1,4,3
	1,3,4,2, 1,4,2,3, 2,1,4,3
	1,2,4,5,3, 1,3,2,5,4
效用圖	1,3,2, 2,1,3, 3,2,1
	1,2,4,3, 1,3,2,4, 1,4,3,2
	1,2,3,5,4, 2,3,1,5,4
	1,2,3,5,4, 2,3,1,5,4

例如，二面體群 是一個 14 個元素的 置換群，它可以由分別對應於反轉和旋轉的兩個元素生成。因此，任何兩個這樣的元素都會給出一個具有 14 個節點和 28 條邊的連通凱萊圖。上面的左圖顯示了生成器選擇為 (7, 1, 2, 3, 4, 5, 6) 和 (7, 6, 5, 4, 3, 2, 1) 的凱萊圖，其中反轉以紅色顯示，旋轉以藍色顯示。任何兩個僅對應於旋轉的元素將給出一個不連通的圖，並且恰好有 15 對這樣的元素，因為有 種方法從六個可能的旋轉中選取兩個元素。（這裡，數字 6 而不是 7 出現，因為單位元素可能不是給出凱萊圖的子集的成員。）右圖顯示了由元素 (7, 1, 2, 3, 4, 5, 6) 和 (6, 7, 1, 2, 3, 4, 5) 生成的 的凱萊圖，該圖是不連通的，因為這些元素不生成該群（特別是，在沒有翻轉的情況下，正階排列無法切換到負階；因此獲得兩個獨立的環）。

上圖顯示了使用元素 (2, 1, 4, 3) 和 (2, 3, 1, 4) 作為生成元的 交錯群 的凱萊圖，它是 截角四面體圖 的有向形式。

如果 完全圖 的三個頂點被不同顏色的石頭覆蓋，並且任何石頭都可以移動到空頂點，則所有位置的圖形成一個凱萊圖，邊表示相鄰位置（左圖）。這對應於 對稱群 的凱萊圖，使用元素 (2, 1, 3, 4)、(3, 2, 1, 4) 和 (4, 2, 3, 1) 作為生成元。結果證明，該圖是唯一具有 24 個頂點的 立方對稱圖 的有向版本（右圖）。

Royle 構建了頂點數不超過 1000 的所有立方凱萊圖，但不包括頂點數為 512 和 768 的圖。

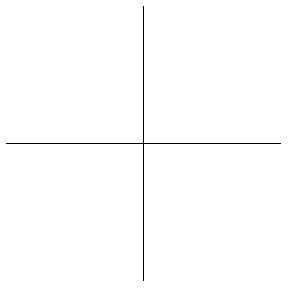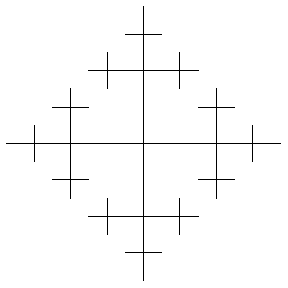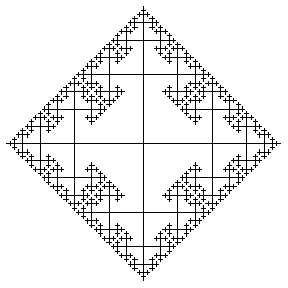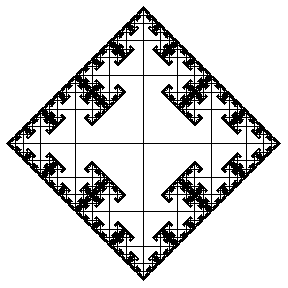
無限群的凱萊圖提供了有趣的幾何形狀。例如，上面說明了兩個生成元上的 自由群 的凱萊圖（繪製到連續級別），分別表示水平和垂直位移。每個新邊都以一半大小繪製，以給出 分形 影像。