主題
Search

四邊形

下載 Mathematica 筆記本下載 Wolfram 筆記本
Quadrilateral

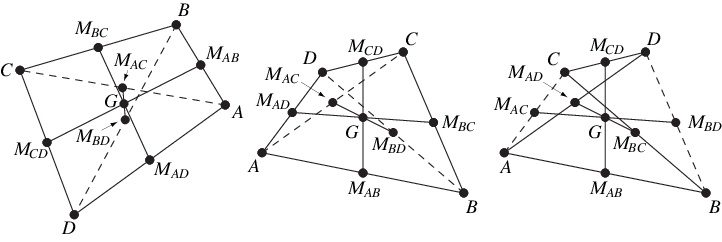
四邊形，有時也稱為四角形或四邊形 (Johnson 1929, p. 61) 是一個四邊多邊形。如果未明確宣告，通常認為所有四個多邊形頂點都位於一個平面內。（如果這些點不位於一個平面內，則該四邊形稱為斜四邊形。）四邊形有三種拓撲型別（Wenninger 1983, p. 50）：凸四邊形（左圖）、凹四邊形（中圖）和交叉四邊形（或蝴蝶形，或領結形；右圖）。

具有兩邊平行的四邊形稱為梯形，而具有對邊平行的四邊形稱為平行四邊形。

QuadrilateralVectors

對於平面凸四邊形（上圖左圖），設邊長為 a、b、c 和 d，半周長 s，以及多邊形對角線 p 和 q。多邊形對角線垂直當且僅當 a^2+c^2=b^2+d^2。

邊長平方和的方程為

a^2+b^2+c^2+d^2=p^2+q^2+4x^2,
(1)

其中 x 是連線多邊形對角線中點的線的長度（Casey 1888, p. 22）。

對於圓內接和外切四邊形，外接圓和內切圓滿足

2r^2(R^2-s^2)=(R^2-s^2)^2-4r^2s^2,
(2)

其中 R 是外接圓半徑，r 是內切圓半徑，s 是圓心距。

給定平面上處於一般位置的任意五個點，其中四個將構成一個凸四邊形。這個結果是所謂的快樂結局問題的一個特例（Hoffman 1998, pp. 74-78）。

對於平面凸四邊形的面積，有一個漂亮的公式，它用其兩條對角線的向量表示。用向量 a、b、c 和 d 表示四邊形的邊，排列方式使得 a+b+c+d=0，並用向量 p 和 q 表示對角線，排列方式使得 p=b+c 和 q=a+b。那麼

K=1/2|det(pq)|
(3)
=1/2|p×q|,
(4)

其中 det(A) 是行列式，pxq 是二維叉積。

對於平面凸四邊形的面積，有許多漂亮的公式，它們用邊長和對角線長度表示，包括

K=1/2pqsintheta
(5)
=1/4(b^2+d^2-a^2-c^2)tantheta
(6)

（Beyer 1987, p. 123），佈雷特施奈德公式

K=1/4sqrt(4p^2q^2-(b^2+d^2-a^2-c^2)^2)
(7)
=sqrt((s-a)(s-b)(s-c)(s-d)-1/4(ac+bd+pq)(ac+bd-pq))
(8)

（Coolidge 1939；Ivanoff 1960；Beyer 1987, p. 123），其中 s 是半周長，以及漂亮的公式

K=sqrt((s-a)(s-b)(s-c)(s-d)-abcdcos^2[1/2(A+B)])
(9)

（Bretschneider 1842；Strehlke 1842；Coolidge 1939；Beyer 1987, p. 123）。

QuadrilateralCentroid

四邊形頂點的質心位於雙中線的交點（即，連線相對中點對的線 M_(AB)M_(CD) 和 M_(AD)M_(BC)）（Honsberger 1995, pp. 36-37）。此外，它也是連線對角線 AC 和 BD 的中點的線 M_(AC)M_(BD) 的中點（Honsberger 1995, pp. 39-40）。

QuadrilateralBisectors

四邊形的四個角平分線在四個共圓點相交（Honsberger 1995, p. 35）。

QuadrilateralTiling

任何非自相交四邊形都可以平鋪平面。

四邊形的四個點之間的六個距離 d_(12)、d_(13)、d_(14)、d_(23)、d_(24) 和 d_(34) 之間存在關係（Weinberg 1972）

0=d_(12)^4d_(34)^2+d_(13)^4d_(24)^2+d_(14)^4d_(23)^2+d_(23)^4d_(14)^2+d_(24)^4d_(13)^2+d_(34)^4d_(12)^2+d_(12)^2d_(23)^2d_(31)^2+d_(12)^2d_(24)^2d_(41)^2+d_(13)^2d_(34)^2d_(41)^2+d_(23)^2d_(34)^2d_(42)^2-d_(12)^2d_(23)^2d_(34)^2-d_(13)^2d_(32)^2d_(24)^2-d_(12)^2d_(24)^2d_(43)^2-d_(14)^2d_(42)^2d_(23)^2-d_(13)^2d_(34)^2d_(42)^2-d_(14)^2d_(43)^2d_(32)^2-d_(23)^2d_(31)^2d_(14)^2-d_(21)^2d_(13)^2d_(34)^2-d_(24)^2d_(41)^2d_(13)^2-d_(21)^2d_(14)^2d_(43)^2-d_(31)^2d_(12)^2d_(24)^2-d_(32)^2d_(21)^2d_(14)^2.
(10)

這可以透過將凱萊-門格爾行列式的左側設定為

288V^2=|0 1 1 1 1; 1 0 d_(12)^2 d_(13)^2 d_(14)^2; 1 d_(21)^2 0 d_(23)^2 d_(24)^2; 1 d_(31)^2 d_(32)^2 0 d_(34)^2; 1 d_(41)^2 d_(42)^2 d_(43)^2 0|
(11)

等於 0（對應於體積為 0 的四面體）來最簡單地推匯出來，從而給出平面四邊形的頂點之間的距離之間的關係（Uspensky 1948, p. 256）。

四邊形的一種特殊型別是圓內接四邊形，對於它，可以外接一個圓，使其與每個多邊形頂點相切。另一種特殊型別是圓外切四邊形，對於它，可以內切一個圓，使其與每條邊相切。既是圓內接又是圓外切的四邊形稱為圓內接和外切四邊形。

另請參閱

反心, 圓內接和外切四邊形, 雙中線, 婆羅摩笈多公式, 佈雷特施奈德公式, 蝴蝶定理, 凱萊-門格爾行列式, 完全四邊形, 圓內接四邊形, 菱形, 八點圓定理, 等腰四邊形, 法諾公理, 萊昂·安妮定理, 菱形, 高線, 垂心四邊形, 平行四邊形, 托勒密定理, 有理四邊形, 矩形, 菱形, 斜四邊形, 正方形, 圓外切四邊形, 梯形, 範·奧貝爾定理, 瓦里尼翁定理, 維滕鮑爾平行四邊形 在 課堂中探索此主題

使用 探索

參考文獻

Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 123, 1987.Bretschneider, C. A. "Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes." Archiv der Math. 2, 225-261, 1842.Casey, J. A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 5th ed., rev. enl. Dublin: Hodges, Figgis, & Co., 1888.Coolidge, J. L. "A Historically Interesting Formula for the Area of a Quadrilateral." Amer. Math. Monthly 46, 345-347, 1939.Dostor, G. "Propriétés nouvelle du quadrilatère en général...." Archiv d. Math. u. Phys. 48, 245-348, 1868.Durell, C. V. "The Quadrilateral and Quadrangle." Ch. 7 in Modern Geometry: The Straight Line and Circle. London: Macmillan, pp. 77-87, 1928.Fukagawa, H. and Pedoe, D. "Circles and Quadrilaterals" and "Quadrilaterals." §3.5 and 4.2 in Japanese Temple Geometry Problems. Winnipeg, Manitoba, Canada: Charles Babbage Research Foundation, pp. 43-45, 47-48, and 125-132, 1989.Harris, J. W. and Stocker, H. "Quadrilaterals." §3.6 in Handbook of Mathematics and Computational Science. New York:Springer-Verlag, pp. 82-86, 1998.Hobson, E. W. A Treatise on Plane and Advanced Trigonometry. New York: Dover, pp. 204-205, 1957.Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.Honsberger, R. "On Quadrilaterals." Ch. 4 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 35-41, 1995.Ivanoff, V. F. "Solution to Problem E1376: Bretschneider's Formula." Amer. Math. Monthly 67, 291-292, 1960.Johnson, R. A. "Quadrangles and Quadrilaterals" and "The Theorem of Ptolemy." §91-92 in Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 61-64, 1929.Routh, E. J. "Moment of Inertia of a Quadrilateral." Quart. J. Pure Appl. Math. 11, 109-110, 1871.Strehlke, F. "Zwei neue Sätze vom ebenen und shparischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes." Archiv der Math. 2, 33-326, 1842.Uspensky, J. V. Theory of Equations. New York: McGraw-Hill, p. 256, 1948.Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, p. 7, 1972.Wenninger, M. J. Dual Models. Cambridge, England: Cambridge University Press, 1983.

在 上被引用

四邊形

請引用為

Eric W. Weisstein "四邊形。" 來自 Web 資源。 https://mathworld.tw/Quadrilateral.html

主題分類