蝴蝶定理

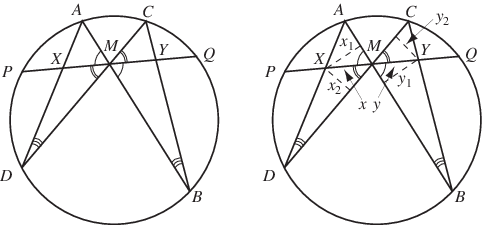
給定圓的一條弦，畫出另外兩條穿過其中點的弦和。將和的交點稱為和。那麼也是的中點。這個定理有很多證明方法，包括 W. G. Horner、Johnson (1929, p. 78) 和 Coxeter (1987, pp. 78 和 144) 的證明。後者簡潔的證明採用了射影幾何。

以下證明由 Coxeter 和 Greitzer (1967, p. 46) 給出。在右圖中，從和向作垂線和，並從和向作垂線和。記，和，然後注意到根據相似三角形

(1)

(2)

(3)

因此

			(4)
			(5)

因此。證畢 (Q.E.D.)

另請參閱

更多嘗試

Bogomolny, A. "蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/Butterfly.shtml.Bogomolny, A. "一個更好的蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/BetterButterfly.shtml.Bogomolny, A. "兩個蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/BetterButterfly.shtml.Coxeter, H. S. M. 射影幾何，第二版 紐約: 施普林格出版社, pp. 78 和 144, 1987.Coxeter, H. S. M. 和 Greitzer, S. L. "蝴蝶定理。" §2.8 in 幾何再探。 華盛頓特區: 美國數學協會, pp. 45-46, 1967.Johnson, R. A. 現代幾何：三角形和圓的幾何學基礎論著。 波士頓, 馬薩諸塞州: 霍頓·米夫林出版社, p. 78, 1929.