基本群

一個弧連通集 的基本群是由所有環路的集合的等價類形成的群，即，起點和終點都在給定的基點 的路徑，在同倫的等價關係下。這個群的單位元是所有與由點 組成的退化路徑同倫的所有路徑的集合。同胚空間的基群是同構的。事實上，基本群只取決於 的同倫型。拓撲空間的基本群由龐加萊引入（Munkres 1993, p. 1）。

以下是一些常見空間 的基本群表格，其中 表示基本群， 是第一個整同調群， 表示群直積， 表示自由積， 表示整數環，並且 是 階的迴圈群。

空間 ()	符號
圓
復射影空間		0	0
8字形
克萊因瓶
-環面
實射影平面
球面		0	0

環路 和 環路 的群乘積 由 的路徑之後跟隨 的路徑給出。單位元由常路徑表示，而 的逆元透過沿相反方向遍歷 給出。基本群與基點的選擇無關，因為透過 的任何環路都與透過任何其他點 的環路同倫。因此，說“ 的基本群”是有意義的。

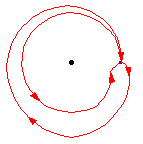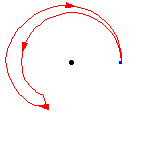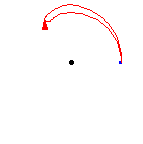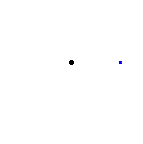
上面的圖表顯示，一個環路後跟相反的環路與常環路同倫，即，單位元。也就是說，它首先遍歷路徑 ，然後調頭並沿另一條路返回，。組合被變形或同倫到常路徑，沿著原始路徑 。

具有平凡基本群（即，每個環路都與常環路同倫）的空間稱為單連通的。例如，任何可收縮空間，如歐幾里得空間，都是單連通的。球面是單連通的，但不是可收縮的。根據定義，萬有覆疊空間 是單連通的，並且 中的環路提升為 中的路徑。萬有覆疊空間中提升的路徑定義了覆蓋變換，它們形成一個與基本群同構的群。

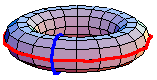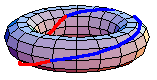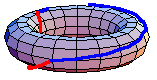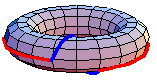
的基本群的底層集合是從圓到 的基於基點的同倫類的集合，表示為 。對於一般的空間 和 ，在 上沒有自然的群結構，但是當存在時， 被稱為餘-H-空間。除了圓之外，每個超球面 都是一個餘-H-空間，定義了同倫群。一般來說，基本群是非阿貝爾群。然而，更高階的同倫群是阿貝爾群。在一些特殊情況下，基本群是阿貝爾群。例如，上面的動畫顯示了在環面中 。紅色路徑在藍色路徑之前進行。該動畫是首先繞內部環的環路和首先繞外部環的環路之間的同倫。

由於第一個整數同調 也由環路表示，環路是唯一沒有邊界的一維物件，因此存在群同態

它是滿射的。事實上， 的群核是換位子群，並且 被稱為阿貝爾化。

當 可以寫成基本群已知的空間的並集 時，可以使用 範·坎彭定理 計算 的基本群。

當 是連續對映時，基本群向前推送。也就是說，存在一個對映 ，其定義為取自 的環路的影像。前推對映是自然的，即，每當定義兩個對映的組合時，。