同倫群將基本群推廣到來自更高維度球體的對映,而不是來自圓的對映。階同倫群,對於拓撲空間
,是來自n-維球面到
的對映的同倫類的集合,具有群結構,並表示為
。基本群是
,並且,如在
的情況下,對映
必須透過基點
。對於
,同倫群
是一個阿貝爾群。
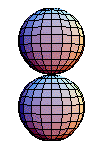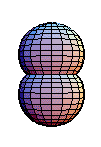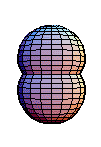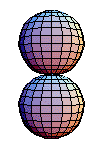
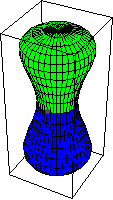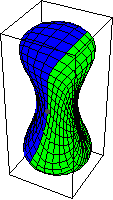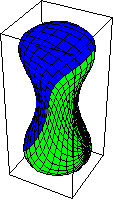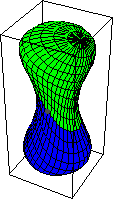
群運算不像基本群的運算那樣簡單。考慮兩個對映 和
,它們都透過
。乘積
透過將赤道對映到基點
給出。然後將北半球透過將赤道坍縮為一個點對映到球面,然後再透過
對映到
。南半球類似地透過
對映到
。上面的圖示顯示了兩個球面的乘積。

單位元由常值對映 表示。基本群中環路方向的選擇對應於同倫群中
的流形定向。因此,對映
的逆對映透過切換球面的定向給出。透過在
座標中描述球面,切換第一和第二座標會改變球面的定向。或者作為超曲面,
,切換定向會反轉內部和外部的角色。上面的圖示表明
與常值對映同倫,即單位元。它首先透過擴充套件
中的赤道開始,然後將結果對映收縮到基點。
與基本群一樣,同倫群不依賴於基點的選擇。但是,高階同倫群始終是阿貝爾群。上面的圖示顯示了 的一個示例。基點是固定的,並且因為
對映可以旋轉。當
,即基本群時,在保持基點固定的同時旋轉對映是不可能的。
對於所有 ,
的空間稱為
-連通的。如果
是
-連通的,
,那麼從
階同倫群到
階同調群的胡列維茨同態
是一個同構。
當 是一個連續對映時,則透過取
下的像來定義
,其中像是
中的球面。前推是自然的,即,只要定義了兩個對映的組合,
。實際上,給定一個纖維化,