覆蓋變換

覆蓋變換，也稱為覆蓋空間變換，對於任何覆蓋 都有定義。它們透過同胚作用於 ，這些同胚保持投影 。覆蓋變換可以透過提升從空間 到其萬有覆蓋 的路徑來定義，萬有覆蓋是一個單連通空間，並且是 的覆蓋。 中的每個環路，比如單位區間上的函式 ，其中 ，提升為 中的路徑，它僅取決於 的選擇，即 的原像中的起始點。此外，端點 僅取決於 的同倫類和 。給定一個點 ，以及 ， 的基本群的一個元素，點 被定義為表示 的路徑 的提升的端點。

萬有覆蓋 的覆蓋變換形成一個群 ，它是商空間的基本群

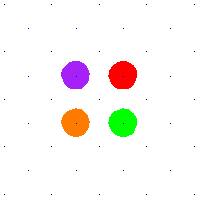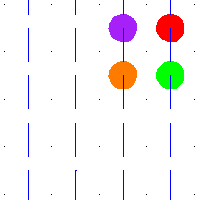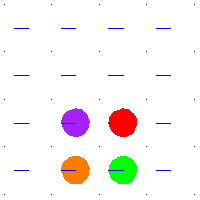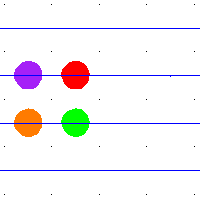
例如，當 是平方環面時，那麼 是平面，並且原像 是整數格點 的平移。環面中的任何環路都提升到平面中的路徑，其端點位於整數格點中。這些平移的整數格點是 在 上透過加法作用的群軌道。上面的動畫展示了一些覆蓋變換在平面上的一些圓盤上的作用。空間是環面及其萬有覆蓋，即平面。基本群的一個元素（藍色路徑所示）定義了萬有覆蓋的一個覆蓋變換。它在萬有覆蓋中移動點。移動後的點在環面中有相同的投影。藍色路徑是環面上的一個環路，並顯示了它的所有原像。