參見
反踏瓣曲線,
負踏瓣曲線,
踏瓣點
使用 探索
參考文獻
Ameseder, A. "Ueber Fusspunktcurven der Kegelschnitte." Archiv Math. u. Phys. 64, 143-144, 1879.Ameseder, A. "Zur Theorie der Fusspunktencurven der Kegelschnitte." Archiv Math. u. Phys. 64, 145-163, 1879.Gray, A. "Pedal Curves." §5.8 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 117-125, 1997.Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 25, 1999.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 46-49 and 204, 1972.Lockwood, E. H. "Pedal Curves." Ch. 18 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 152-155, 1967.Porteous, I. R. Geometric Differentiation for the Intelligence of Curves and Surfaces. Cambridge, England: Cambridge University Press, 1994.Trott, M. The Mathematica GuideBook for Graphics. New York: Springer-Verlag, p. 19, 2004. http://www.mathematicaguidebooks.org/.Ueda, K. In Mathematical Methods for Curves and Surfaces (Ed. T. Lyche and L. L. Shumaker). Nashville, TN: Vanderbilt University Press, 2001.Yates, R. C. "Pedal Curves." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 160-165, 1952.Zwikker, C. The Advanced Geometry of Plane Curves and Their Applications. New York: Dover, pp. 150-158, 1963.在 中被引用
踏瓣曲線
請引用為
韋斯坦因,埃裡克·W. "踏瓣曲線。" 來自 網路資源。 https://mathworld.tw/PedalCurve.html
主題分類
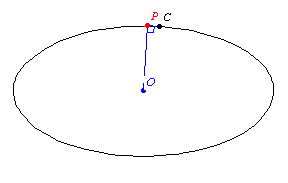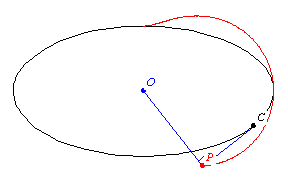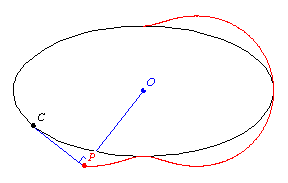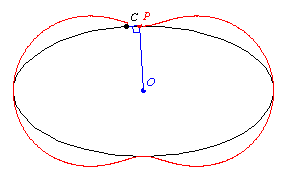
關於點
的踏瓣曲線是從
到曲線切線的垂足的軌跡。更準確地說,給定曲線
,關於固定點
(稱為踏瓣點)的
的踏瓣曲線
是從
到
的切線的垂線的交點
的軌跡。相對於踏瓣點
,曲線
的引數方程由下式給出
是曲線
的踏瓣曲線,則
是
的負踏瓣曲線 (Lawrence 1972, pp. 47-48)。