輪盤線是由附著在一個閉合凸曲線上的一個固定點,當該曲線沿第二條曲線無滑動滾動時所描繪出的曲線。當圓錐曲線的焦點在直線上滾動時所描述的輪盤線是最小曲面的截面(即,當圍繞直線旋轉時,它們產生最小曲面),被稱為波紋面。
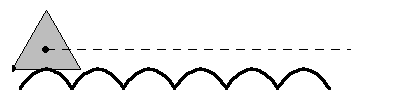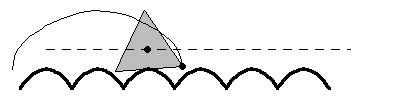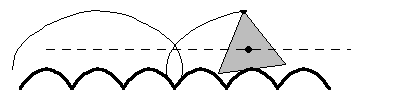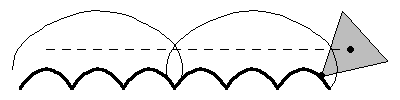
輪盤線一個特別有趣的例子是一個正  邊形在一個由一系列截斷的懸鏈線組成的“道路”上滾動,如上圖所示,這是 Robison (1960) 首先提出的。這種運動是平滑的,因為幾何中心遵循一條直線,儘管在滾動等邊三角形的情況下,物理模型將不可能構建,因為三角形的頂點會“卡”在轍跡中 (Wagon 2000)。對於滾動的正方形(“方形輪”),道路的形狀是懸鏈線
邊形在一個由一系列截斷的懸鏈線組成的“道路”上滾動,如上圖所示,這是 Robison (1960) 首先提出的。這種運動是平滑的,因為幾何中心遵循一條直線,儘管在滾動等邊三角形的情況下,物理模型將不可能構建,因為三角形的頂點會“卡”在轍跡中 (Wagon 2000)。對於滾動的正方形(“方形輪”),道路的形狀是懸鏈線  在
在  處截斷 (Wagon 2000)。有趣的是,J. C. 麥克斯韋(電磁理論的著名人物)在 1849 年發表了一份詳細的數學分析 (Maxwell 1849),雖然它沒有包含截斷懸鏈線的關鍵思想,但基本上包含了所有其他潛在的數學思想。
處截斷 (Wagon 2000)。有趣的是,J. C. 麥克斯韋(電磁理論的著名人物)在 1849 年發表了一份詳細的數學分析 (Maxwell 1849),雖然它沒有包含截斷懸鏈線的關鍵思想,但基本上包含了所有其他潛在的數學思想。
對於正  邊形,對應懸鏈線的笛卡爾方程是
邊形,對應懸鏈線的笛卡爾方程是
其中

在 Wagon (2000) 的封面上描繪了正方形在截斷懸鏈線道路上的輪盤線。
給定一條基曲線,讓另一條曲線在其上滾動,並將剛性連線到這條滾動曲線的點稱為“極點”。下表總結了各種常見曲線和極點的輪盤線。請注意,短幅擺線、擺線和長幅擺線統稱為旋輪線,外擺線(稱為外旋輪線)和內擺線(稱為內旋輪線)的各種變體也是如此。
另請參閱
懸鏈線、
三角曲線、
滑移線、
勒洛多邊形、
勒洛三角形、
轉子、
波紋面
使用 探索
參考文獻
Besant, W. H. Notes on Roulettes and Glissettes, 2nd enl. ed. Cambridge, England: Deighton, Bell & Co., 1890.Cundy, H. and Rollett, A. "Roulettes and Involutes." §2.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 46-55, 1989.Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 128, 1984.Hall, L. and Wagon, S. "Roads and Wheels." Math. Mag. 65, 283-301, 1992.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 56-58 and 206, 1972.Lockwood, E. H. "Roulettes." Ch. 17 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 138-151, 1967.Maxwell, J. C. "On the Theory of Rolling Curves." §XXXV in Trans. Roy. Soc. Edin. 16, 519-540, 1849.Robison, G. B. "Rockers and Rollers." Math. Mag. 33, 139-144, 1960.Wasgon, S. "The Ultimate Flat Tire." Math. Horizons, pp. 14-17, Feb. 1999.Wagon, S. Mathematica in Action, 2nd ed. New York: W. H. Freeman, p. 52, 2000.Yates, R. C. "Roulettes." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 175-185, 1952.Zwillinger, D. (Ed.). "Roulettes (Spirograph Curves)." §8.2 in CRC Standard Mathematical Tables and Formulae, 3rd ed. Boca Raton, FL: CRC Press, 1996.在 上被引用
輪盤賭
請引用為
Weisstein, Eric W. "輪盤賭。" 來自 Web 資源。 https://mathworld.tw/Roulette.html
主題分類

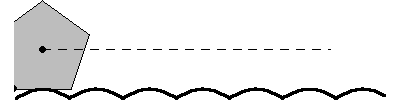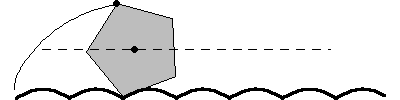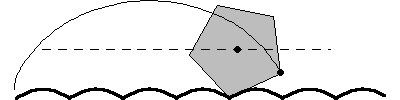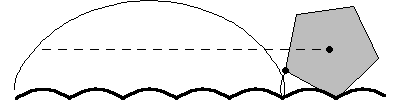

邊形在一個由一系列截斷的懸鏈線組成的“道路”上滾動,如上圖所示,這是 Robison (1960) 首先提出的。這種運動是平滑的,因為幾何中心遵循一條直線,儘管在滾動等邊三角形的情況下,物理模型將不可能構建,因為三角形的頂點會“卡”在轍跡中 (Wagon 2000)。對於滾動的正方形(“方形輪”),道路的形狀是懸鏈線
在
處截斷 (Wagon 2000)。有趣的是,J. C. 麥克斯韋(電磁理論的著名人物)在 1849 年發表了一份詳細的數學分析 (Maxwell 1849),雖然它沒有包含截斷懸鏈線的關鍵思想,但基本上包含了所有其他潛在的數學思想。
邊形,對應懸鏈線的笛卡爾方程是
