主題
Search

拋物線

下載 Mathematica 筆記本下載 Wolfram 筆記本
ParabolaDirectrix

拋物線（複數形式為“拋物線”；Gray 1997，第 45 頁）是在平面內所有點組成的集合，這些點到給定直線 L ( 圓錐曲線準線 ) 和給定點 F （不在直線上的焦點）的距離相等。焦引數（即準線和焦點之間的距離）因此由 p=2a 給出，其中 a 是從頂點到準線或焦點的距離。透過圍繞對稱軸旋轉拋物線獲得的旋轉曲面稱為拋物面。

ParabolaFocus

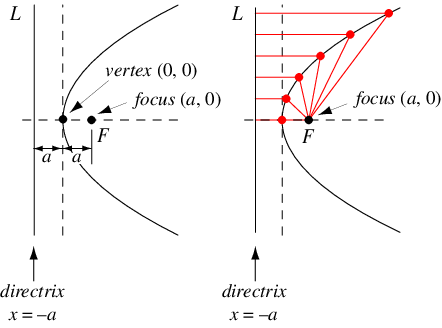
梅內克繆斯研究了拋物線，試圖實現倍立方。梅內克繆斯透過找到兩個拋物線 x^2=y 和 y^2=2x 的交點解決了這個問題。歐幾里得寫了關於拋物線的文章，阿波羅尼奧斯給它起了現在的名字。帕斯卡將拋物線視為圓的投影，伽利略表明在均勻重力下，拋射體的軌跡是拋物線。格雷戈裡和牛頓考慮了拋物線的折射線性質，即把平行光線匯聚到一個焦點上（MacTutor 檔案館），如上圖所示。

對於頂點在 (0, 0) 且開口向右的拋物線，笛卡爾座標系中的方程為

sqrt((x-a)^2+y^2)=x+a
(1)
(x-a)^2+y^2=(x+a)^2
(2)
x^2-2ax+a^2+y^2=x^2+2ax+a^2
(3)
y^2=4ax.
(4)

量 4a 被稱為焦弦。

如果頂點在 (x_0,y_0) 而不是 (0, 0)，則焦弦為 a 的拋物線方程為

(y-y_0)^2=4a(x-x_0).
(5)

頂點在 (x_0,y_0) 且焦弦為 a 的開口向上的拋物線方程為

(x-x_0)^2=4a(y-y_0).
(6)
Parabola3Points

三個點唯一確定一個準線平行於 x 軸的拋物線和一個準線平行於 y 軸的拋物線。如果這些拋物線透過三個點 (x_1,y_1)、(x_2,y_2) 和 (x_3,y_3)，則它們的方程由下式給出

|x^2 x y 1; x_1^2 x_1 y_1 1; x_2^2 x_2 y_2 1; x_3^2 x_3 y_3 1|=0
(7)

和

|y^2 x y 1; y_1^2 x_1 y_1 1; y_2^2 x_2 y_2 1; y_3^2 x_3 y_3 1|=0.
(8)
ParabolaPolar

在極座標系中，引數為 a 且中心為 (0, 0) 的拋物線方程由下式給出

r=-(2a)/(1+costheta)
(9)

（左圖）。透過建立座標系 (x^',y^')=(x-a,y) 並代入 r=sqrt(x^('2)+y^('2)) 和 theta=tan^(-1)(y^'/x^') 可以看出與笛卡爾形式的等價性，得到

sqrt((x-a)^2+y^2)=-(2a)/(1+(x-a)/(sqrt((x-a)^2+y^2))).
(10)

展開並收集項，

a+x+sqrt((a-x)^2+y^2)=0,
(11)

因此求解 y^2 得到 (◇)。一組共焦拋物線顯示在右圖中。

在垂足座標系中，垂足點位於焦點時，方程為

p^2=ar.
(12)

拋物線可以引數化地寫成

x=at^2
(13)
y=2at
(14)

或

x=(t^2)/(4a)
(15)
y=t.
(16)

拋物線段是李薩如圖形。

ParabolaEnvelope

拋物線可以透過連線兩條線段上的相對點來生成為兩條相交線段的包絡線（Wells 1991）。

ParabolaTangents

在上圖中，直線 SPA、SQB 和 POQ 分別在點 A、B 和 O 處與拋物線相切。然後 SP/PA=QO/OP=BQ/QS (Wells 1991)。此外，DeltaPQS 的外接圓透過焦點 F (Honsberger 1995，第 47 頁)。此外，從焦點到拋物線切線的垂足始終位於頂點處的切線上（Honsberger 1995，第 48 頁）。

ParabolaTangentLines

給定一個位於拋物線“外部”的任意點 P，可以透過繪製以 PF 為直徑的圓來構造透過 P 的拋物線切線或切線，其中 F 是焦點。然後找到圓與透過 V 的垂直切線相交的點 A 和 B。點 T_A 和 T_B （在退化情況下可以坍縮為單點）然後是直線 PA 和 PB 與拋物線的切點 (Wells 1991)。

曲率、弧長和切線角為

kappa(t)=1/(2a(1+t^2)^(3/2))
(17)
s(t)=a(tsqrt(1+t^2)+sinh^(-1)t)
(18)
phi(t)=tan^(-1)t.
(19)

拋物線的切向量為

x_T(t)=1/(sqrt(1+t^2))
(20)
y_T(t)=t/(sqrt(1+t^2)).
(21)

下圖顯示了拋物線的法向量和切向量。

ParabolaNormalTangent

另請參見

圓錐曲線、橢圓、雙曲線、拋物線折射線、拋物線漸屈線、拋物線反演曲線、拋物線漸伸線、拋物線負垂足曲線、拋物線垂足曲線、拋物面、二次曲線、反射性質、契爾恩豪森三次垂足曲線、韋爾奇窗函式 在 課堂中探索此主題

使用 探索

參考文獻

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 198 and 222-223, 1987.Casey, J. "The Parabola." Ch. 5 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.Coxeter, H. S. M. "Conics." §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 4, 1999.Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 47-48, 1995.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.Lockwood, E. H. "The Parabola." Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 2-12, 1967.Loomis, E. S. "The Parabola." §2.5 in The Pythagorean Proposition: Its Demonstrations Analyzed and Classified and Bibliography of Sources for Data of the Four Kinds of "Proofs," 2nd ed. Reston, VA: National Council of Teachers of Mathematics, pp. 25-28, 1968.MacTutor History of Mathematics Archive. "Parabola." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.Pappas, T. "The Parabolic Ceiling of the Capitol." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 22-23, 1989.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 169-172, 1991.Yates, R. C. "Conics." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.

請引用為

Weisstein, Eric W. "拋物線。" 來源： Web 資源。 https://mathworld.tw/Parabola.html

主題分類