雙曲線

雙曲線（複數形式為“hyperbolas”；Gray 1997, p. 45）是一個 圓錐截面，定義為所有點 在 平面 內的 軌跡，這些點到兩個固定點（焦點 和 ）的距離 和 之差的絕對值，這兩個固定點相距 ，是一個給定的 正 常數 ,

（Hilbert 和 Cohn-Vossen 1999, p. 3）。令點 落在左側 -截距上，則要求

因此常數由 給出，即 -截距之間的距離（上圖左側）。雙曲線具有一個重要的性質：從一個 焦點 發出的光線，以某種方式反射，使得出射路徑沿著從另一個 焦點 穿過交點的直線（上圖右側）。

等軸雙曲線 的特殊情況，對應於離心率 的雙曲線，最早由 Menaechmus 研究。歐幾里得和阿里斯泰俄斯寫了關於一般雙曲線的文章，但只研究了它的一支。雙曲線的現名由阿波羅尼奧斯給出，他是第一個研究雙曲線兩支的人。焦點 和 圓錐曲線準線 由帕普斯考慮（MacTutor 檔案館）。雙曲線是逃逸軌跡上物體的軌道形狀（即具有正能量的物體），例如一些彗星，圍繞一個固定質量的物體，例如太陽。

雙曲線可以透過連線剛性杆 的自由端 來構造，其中 是一個 焦點，另一個 焦點 用繩子 連線。當杆 繞 旋轉，並且 保持緊貼杆（即位於杆上）時， 的 軌跡 是雙曲線的一個分支（上圖左側；Wells 1991）。阿波羅尼奧斯定理指出，對於在點 與雙曲線相切，並在點 和 與漸近線 相交 的線段，則 是常數，且 （上圖右側；Wells 1991）。

設雙曲線上的點 的笛卡爾座標為 ，則雙曲線的定義 給出

重新排列並完成平方項得到

兩邊同時除以 得到

與 橢圓 的定義類比，定義

因此，半長軸 平行於 x 軸，半短軸 平行於 y 軸 的雙曲線方程由下式給出：

或者，對於中心在點 而不是 的情況，方程為：

與 橢圓 不同，雙曲線沒有點實際位於 半短軸 上，而是比率 決定了雙曲線的垂直縮放。離心率 （總是滿足 ）定義為：

在雙曲線的標準方程中，中心位於 ，焦點 位於 ，頂點位於 。所謂的 漸近線 （在上圖中以虛線顯示）可以透過將通用方程 (8) 右側的 1 替換為 0 找到：

因此，斜率 為 。

的特殊情況（上圖左側）被稱為 等軸雙曲線，因為 漸近線 是 互相垂直 的。

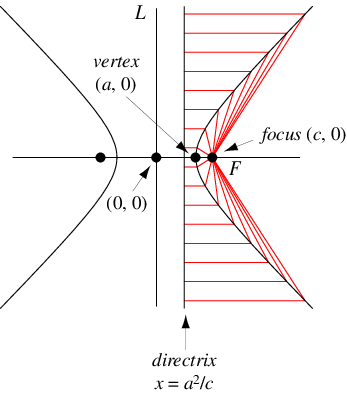
雙曲線也可以定義為點的 軌跡，這些點到 焦點 的距離與到垂直線 （稱為 圓錐曲線準線）的水平距離成比例，其中比例 。設 為比例， 為準線到中心的距離，則

其中 因此僅僅是 離心率 。

像非圓形 橢圓 一樣，雙曲線有兩個不同的 焦點 和兩個相關的 圓錐曲線準線，每個 圓錐曲線準線 都 垂直於 連線兩個焦點的直線 (Eves 1965, p. 275)。

雙曲線的 焦引數 為

在 極座標 中，中心位於 原點 的雙曲線方程（即 ）為

在以 焦點 為中心的 極座標 中，

如上圖所示。

以 焦點 為原點的雙中心 雙極座標 方程為

雙曲線右支的 引數方程 由下式給出：

其中 是 雙曲餘弦， 是 雙曲正弦，它們覆蓋了雙曲線的右支。

覆蓋雙曲線兩個分支的引數表示為

其中 ，在 處不連續。上述引數化的 弧長、曲率 和 切線角 為

其中 是 第二類橢圓積分。

雙曲線的 特殊仿射曲率 為

包含固定在三維空間中的 橢圓 的可變 圓錐 的頂點的 軌跡 是透過 橢圓 的 焦點 的雙曲線。此外，包含該雙曲線的 圓錐 的頂點的 軌跡 是原始 橢圓。此外，橢圓 和雙曲線的 離心率 互為倒數。