主題
Search

橢圓

下載 Mathematica Notebook下載 Wolfram Notebook
EllipseBipolar
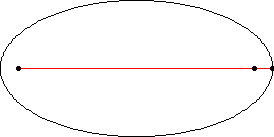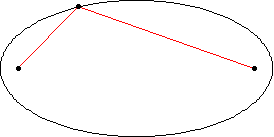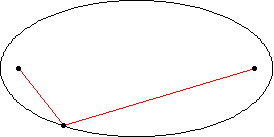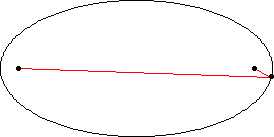
Ellipse construction

橢圓是一條曲線，它是軌跡，由平面內所有點組成，這些點到兩個固定點 F_1 和 F_2 （焦點）的距離 r_1 和 r_2 之和為一個給定的正常數 2a （Hilbert 和 Cohn-Vossen 1999, p. 2）。這導致雙中心雙極座標方程

r_1+r_2=2a,
(1)

其中 a 是半長軸，座標系的原點位於其中一個焦點。相應的引數 b 被稱為半短軸。

橢圓是圓錐曲線和利薩如曲線。

可以使用Wolfram 語言指定橢圓，使用Circle[{x, y}, {a, b}].

如果線段的端點沿著兩條相交線移動，則線段上（或延長線上）的固定點會描繪出橢圓的弧。這被稱為橢圓的橢圓規作圖法（Eves 1965, p. 177）。

Elliptic gears

可以構造橢圓齒輪，使其彼此平穩旋轉（Brown 1871, pp. 14-15; Reuleaux 和 Kennedy 1876, p. 70; Clark 和 Downward 1930; KMODDL）。

橢圓最早由 Menaechmus 研究，由歐幾里得研究，並由阿波羅尼奧斯命名。焦點和橢圓的圓錐曲線準線由帕普斯考慮。1602 年，開普勒認為火星的軌道是卵形的；他後來發現它是一個橢圓，太陽位於一個焦點上。事實上，開普勒引入了“焦點”一詞，並在 1609 年發表了他的發現。1705 年，哈雷表明，現在以他的名字命名的彗星以橢圓軌道繞太陽執行（MacTutor Archive）。橢圓繞其短軸旋轉產生扁球體，而橢圓繞其長軸旋轉產生長球體。

穿過焦點的光線在單次反射後將穿過另一個焦點（Hilbert 和 Cohn-Vossen 1999, p. 3）。不穿過焦點的反射將與共焦雙曲線或橢圓相切，具體取決於光線是否穿過焦點之間。

讓橢圓沿 x 軸延伸，並找到圖形的方程 (1)，其中 F_1 和 F_2 位於 (-c,0) 和 (c,0)。在笛卡爾座標系中，

sqrt((x+c)^2+y^2)+sqrt((x-c)^2+y^2)=2a.
(2)

sqrt((x+c)^2+y^2)+sqrt((x-c)^2+y^2)=2a

(x+c)^2+y^2=4a^2-4asqrt((x-c)^2+y^2)+(x-c)^2+y^2.
(3)

將第二項移到右側並平方兩側，

sqrt((x-c)^2+y^2)=-1/(4a)(x^2+2xc+c^2+y^2-4a^2-x^2+2xc-c^2-y^2)
(4)
=-1/(4a)(4xc-4a^2)
(5)
=a-c/ax.
(6)

(x+c)^2+y^2=(2a-sqrt((x-c)^2+y^2))^2

x^2-2xc+c^2+y^2=a^2-2cx+(c^2)/(a^2)x^2.
(7)

現在求解平方根項並簡化

x^2(a^2-c^2)/(a^2)+y^2=a^2-c^2,
(8)

sqrt((x-c)^2+y^2)=a-(cx)/a

(x^2)/(a^2)+(y^2)/(a^2-c^2)=1.
(9)

最後平方一次以消除剩餘的平方根，

b^2=a^2-c^2
(10)

(x-c)^2+y^2=(a-(cx)/a)^2

(x^2)/(a^2)+(y^2)/(b^2)=1.
(11)

將 x 項分組，然後得到

如果橢圓的中心不是位於 (0, 0)，而是位於 (x_0, y_0)，則方程 (◇) 變為

((x-x_0)^2)/(a^2)+((y-y_0)^2)/(b^2)=1.
(12)

((x-x_0)^2)/(a^2)+((y-y_0)^2)/(b^2)=1

x=acost
(13)
y=bsint.
(14)

從橢圓的笛卡爾方程可以看出，該曲線也可以用一個簡單的引數形式給出，類似於圓的引數形式，但 x 和 y 座標具有不同的縮放比例，

ax^2+2bxy+cy^2+2dx+2fy+g=0
(15)

x=acost

Delta=|a b d; b c f; d f g|
(16)
J=|a b; b c|
(17)
I=a+c,
(18)

y=bsint

x_0=(cd-bf)/(b^2-ac)
(19)
y_0=(af-bd)/(b^2-ac),
(20)

一般的二次曲線

a^'=sqrt((2(af^2+cd^2+gb^2-2bdf-acg))/((b^2-ac)[sqrt((a-c)^2+4b^2)-(a+c)]))
(21)
b^'=sqrt((2(af^2+cd^2+gb^2-2bdf-acg))/((b^2-ac)[-sqrt((a-c)^2+4b^2)-(a+c)])).
(22)

Ax^2+Bxy+Cy^2+Dx+Ey+F=0

phi={0 for b=0 and a<c; 1/2pi for b=0 and a>c; 1/2cot^(-1)((a-c)/(2b)) for b!=0 and a<c; pi/2+1/2cot^(-1)((a-c)/(2b)) for b!=0 and a>c.
(23)
EllipseDirectrix

當在定義之後是橢圓

r=(a-c)/(d-a)=(sqrt(b^2+c^2))/d.
(24)

Delta=|(A,B/2,D/2),(B/2,C,E/2),(D/2,E/2,F)|

d=(a^2)/(sqrt(a^2-b^2))=(a^2)/c
(25)
r=(sqrt(a^2-b^2))/a=c/a.
(26)

Delta!=0, J>0, 和 Delta/I<0。還假設橢圓是非退化的（即，它不是一個圓，所以 a!=c，並且我們已經確定它不是一個點，因為 J=ac-b^2!=0）。在這種情況下，橢圓的中心 (x_0,y_0) 由下式給出

p=(b^2)/(sqrt(a^2-b^2))
(27)
=(a^2-c^2)/c
(28)
=(a(1-e^2))/e,
(29)

x_0=(2CD-BE)/(B^2-4AC)

Ellipse4Points

y_0=(2AE-BD)/(B^2-4AC)

|x^2 y^2 x y 1; x_1^2 y_1^2 x_1 y_1 1; x_2^2 y_2^2 x_2 y_2 1; x_3^2 y_3^2 x_3 y_3 1; x_4^2 y_4^2 x_4 y_4 1|=0.
(30)

半軸長度為

s_1s_2s_3+s_1s_2s_4+s_1s_3s_4+s_2s_3s_4-(s_1+s_2+s_3+s_4)=0,
(31)

a^2=(2Delta)/(J(sqrt((A-C)^2+B^2)-(A+C)))

(s_1^4+s_2^4+s_3^4+s_4^4)+(4s_2^2s_3^2s_1^2+s_2^2s_4^2s_1^2+s_3^2s_4^2s_1^2+s_2^2s_3^2s_4^2)-4(s_2s_3s_4s_1^3+s_2s_3s_4^3s_1+s_2s_3^3s_4s_1+s_2^3s_3s_4s_1)-2(s_2^2s_1^2+s_3^2s_1^2+s_4^2s_1^2+s_2^2s_3^2+s_2^2s_4^2-2s_3^2s_4^2)+8s_2s_3s_4s_1. =0
(32)

b^2=(2Delta)/(J(-sqrt((A-C)^2+B^2)-(A+C)))

從 x 軸到橢圓長軸的逆時針旋轉角為

e=sqrt(1-(b^2)/(a^2)),
(33)

theta={1/2}cot^(-1)((A-C)/B)

b=asqrt(1-e^2)
(34)
=sqrt(a^2-c^2)
(35)
c=sqrt(a^2-b^2)
(36)
=ae
(37)
e=sqrt(1-(b^2)/(a^2))
(38)
=c/a.
(39)

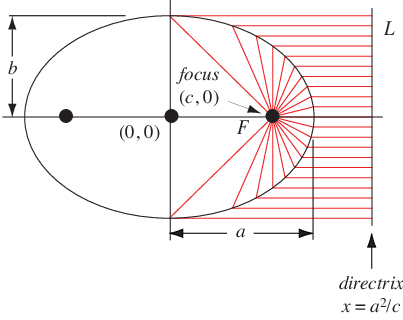
橢圓也可以定義為點的軌跡，這些點到焦點的距離與到稱為圓錐曲線準線的垂直線的水平距離成比例，其中比率為 <1。令 r 為比率，d 為準線與中心的距離，那麼為了使此成立，它必須在長軸和短軸的極值處成立，因此

EllipseFocus

a=rd

x=c+rcostheta
(40)
y=rsintheta,
(41)

sqrt(a^2-b^2)=r(d-b^2/a)

((c+rcostheta)^2)/(a^2)+(r^2sin^2theta)/(b^2)=1.
(42)

求解得到

b^2(c^2+2crcostheta+r^2cos^2theta)+a^2r^2sin^2theta=a^2b^2.
(43)

r=sqrt(1-b^2/a^2)

b^2c^2+2rcb^2costheta+b^2r^2cos^2theta+a^2r^2-a^2r^2cos^2theta=a^2b^2.
(44)

d=a

a^2(1-e^2)a^2e^2+2aea^2(1-e^2)rcostheta+a^2(1-e^2)r^2cos^2theta +a^2r^2-a^2r^2cos^2theta=a^2[a^2(1-e^2)].
(45)

橢圓的焦引數是

-r^2+[ercostheta-a(1-e^2)]^2=0,
(46)

p=b^2/a

r=+/-[ercostheta-a(1-e^2)].
(47)

其中 e 是橢圓的一個特徵，稱為離心率，稍後將定義。

r=a(1-e^2)-ercostheta
(48)
r(1+ecostheta)=a(1-e^2)
(49)
r=(a(1-e^2))/(1+ecostheta).
(50)
Ellipsex

軸線平行於座標軸的橢圓由其上的任意四個非共圓點唯一確定，並且透過四個點 (x_1,y_1), (x_2,y_2), (x_3,y_3), 和 (x_4,y_4) 的橢圓的方程為

costheta=(x-c)/r.
(51)

|x^2,y^2,x,y,1,(x_1^2,y_1^2,x_1,y_1,1),(x_2^2,y_2^2,x_2,y_2,1),(x_3^2,y_3^2,x_3,y_3,1),(x_4^2,y_4^2,x_4,y_4,1)|=0

r+e(x-c)=a(1-e^2)
(52)
r=a(1-e^2)-e(x-c).
(53)

令軸線平行於座標軸的橢圓上的四個點的角座標為 t_i，其中 i=1, 2, 3 和 4。當

(b^2)/(p^2)=(2a)/r-1.
(54)

(s_1-s_3)(s_2-s_4)=(s_1-s_4)(s_2-s_3)

s(t)=aE(t,e)
(55)
=aE(t,sqrt(1-(b^2)/(a^2)))
(56)
=bE(t,sqrt(1-(a^2)/(b^2))),
(57)

當中間變數 s_i=tan(t_i/2) 已被定義時，這些點是共圓的（Berger et al. 1984; Trott 2006, pp. 39-40）。相當令人驚訝的是，在簡化上述公式後，得到相同的關係，其中 s_i 現在被解釋為 s_i=sin(t_i)。一個等效但更復雜的條件由下式給出

sin(t_1+t_3)sint_2sint_4=sin(t_2+t_4)sint_1sint_3

theta=tan^(-1)(y/x)=tan^(-1)(b/atant).
(58)
EllipseFunction

與雙曲線一樣，非圓橢圓有兩個不同的焦點和兩個相關的準線，每個圓錐曲線準線都垂直於連線兩個焦點的直線（Eves 1965, p. 275）。

kappa(t)=(ab)/((b^2cos^2t+a^2sin^2t)^(3/2))
(59)
phi(t)=tan^(-1)(a/btant).
(60)

定義一個新常數 0<=e<1，稱為離心率（其中 e=0 是圓的情況）以替換 b

p=aE(2pi,e)
(61)
=4aE(1/2pi,e)
(62)
=4aE(e),
(63)

e=sqrt(1-b^2/a^2)

p=pi(a+b)sum_(n=0)^(infty)(1/2; n)^2h^(2n)
(64)
=pi(a+b)(1+1/4h^2+1/(64)h^4+1/(256)h^6+...)
(65)

由此得出

h=(a-b)/(a+b).
(66)

b^2=a^2(1-e^2)

p=pi(a+b)_2F_1(-1/2,-1/2;1;h^2)
(67)
=2(a+b)[2E(h)+2(h^2-1)K(h)],
(68)

c=ae

EllipsePerimeter

p=a(1-e^2)

p approx pisqrt(2(a^2+b^2))
(69)
approx pi[3(a+b)-sqrt((a+3b)(3a+b))]
(70)
approx pi(a+b)(1+(3h)/(10+sqrt(4-3h))),
(71)

d=a/e

r=1-e

r_+=r_(apoapsis)=a(1+e)
(72)
r_-=r_(periapsis)=a(1-e).
(73)

r=1+e

A=int_(-a)^aint_(-bsqrt(a^2-x^2)/a)^(bsqrt(a^2-x^2)/a)dydx
(74)
=int_(-a)^a(2b)/asqrt(a^2-x^2)dx
(75)
=(2b)/a{1/2[xsqrt(a^2-x^2)+a^2sin^(-1)(x/(|a|))]}_(x=-a)^a
(76)
=ab[sin^(-1)1-sin^(-1)(-1)]
(77)
=ab[pi/2-(-pi/2)]
(78)
=piab.
(79)

e=c/a

1/(a^2)(a/bx^')^2+(y^('2))/(b^2)=1,
(80)

離心率因此可以解釋為焦點的位置，表示為半長軸的一部分。

(partialx)/(partialx^')=((partialx^')/(partialx))^(-1)=(b/a)^(-1)=a/b,
(81)

如果從焦點 F 而不是從中心 C 測量 r 和 theta （在軌道力學中通常是這樣），則橢圓方程為

|(partial(x,y))/(partial(x^',y^'))|=|(partialx)/(partialx^') (partialy)/(partialx^'); (partialx)/(partialy^') (partialy)/(partialy^')|
(82)
=|a/b 0; 0 1|=a/b.
(83)

x=r(theta)costheta+ae

intint_(R)dxdy=intint_(R^')|(partial(x,y))/(partial(x^',y^'))|dx^'dy^'
(84)
=a/bintint_(R^')dx^'dy^'
(85)
=a/b(pib^2)
(86)
=piab,
(87)

y=r(theta)sintheta

ax^2+bxy+cy^2=1
(88)

並且 (◇) 變為

A=(2pi)/(sqrt(4ac-b^2)).
(89)

(r(theta)costheta+ae)^2/a^2+(r(theta)sintheta)^2/b^2=1

A=1/2pi(a^2+b^2+|OP|^2).
(90)
EllipseNormalTangent

清除分母得到

x_T(t)=-(asint)/(sqrt(b^2cos^2t+a^2sin^2t))
(91)
y_T(t)=(bcost)/(sqrt(b^2cos^2t+a^2sin^2t)).
(92)

b^2(r(theta)costheta+ae)^2+a^2(r(theta)sintheta)^2=a^2b^2

代入 sin^2theta=1-cos^2theta 得到

b^2(rcostheta+ae)^2+a^2r^2(1-cos^2theta)=a^2b^2

代入以用 a 和 e 重新表達 b 和 c,

a^2(1-e^2)(rcostheta+ae)^2+a^2r^2(1-cos^2theta)=a^4(1-e^2)

r=(a(1-e^2))/(1+ecostheta)

符號可以透過要求 r 必須為正來確定。當 e=0 時，(47) 變為 r=+/-(-a)，但由於 a 始終為正，我們必須取負號，因此 (47) 變為

引用為

Weisstein, Eric W. "Ellipse." 來自 Web 資源。 https://mathworld.tw/Ellipse.html

主題分類