雙曲直角

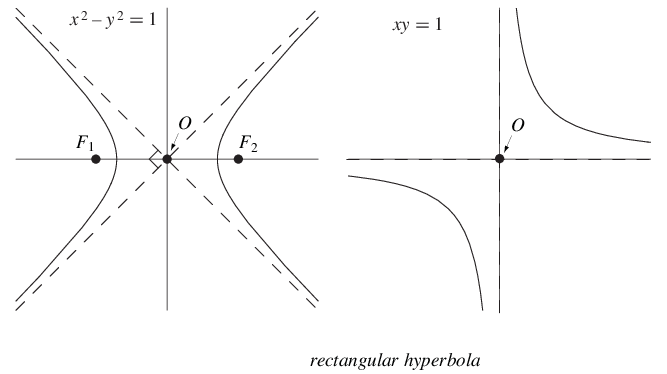
一種雙曲線，其漸近線是垂直的，也稱為等邊雙曲線或直角雙曲線。當半長軸和半短軸相等時，就會發生這種情況。這對應於取，得到離心率。將代入雙曲線的一般方程，其中半長軸平行於x軸，半短軸平行於y軸（即，垂直圓錐曲線準線），

(1)

因此得到

(2)

向左和向右開口的雙曲直角具有極座標方程

(3)

並且在第一象限和第三象限開口的雙曲直角具有笛卡爾方程

(4)

雙曲直角右分支的引數方程由下式給出

			(5)
			(6)

其中是雙曲餘弦，是雙曲正弦。對於上述引數化，當時，曲率、弧長和切線角為

			(7)
			(8)
			(9)
			(10)
			(11)

其中是第二類橢圓積分，是伽馬函式，是超幾何函式，是不完全貝塔函式，是雙曲正切。

給出兩個分支的引數化由下式給出

			(12)
			(13)

其中，並且在處不連續。

中心位於雙曲線中心的反演中心的雙曲直角的反曲線是伯努利雙紐線 (Wells 1991)。

如果三角形的三個頂點位於雙曲直角上，那麼垂心也位於其上 (Wells 1991)。等效地，如果四個點形成一個垂心繫統，那麼存在一個透過這些點的雙曲直角族。此外，這些雙曲線的中心的軌跡是三角形的九點圓 (Wells 1991)。

如果四個點不形成垂心繫統，那麼存在一個唯一的透過它們的雙曲直角，並且其中心由每次取三個點的點的九點圓的交點給出 (Wells 1991)。