 |  |  |
(1)
|
 |  |  |
(2)
|
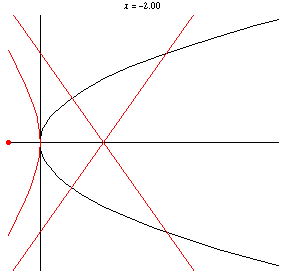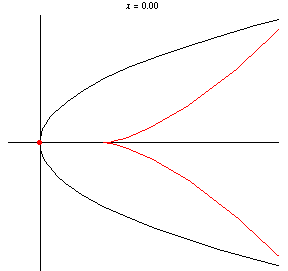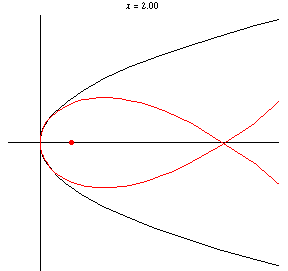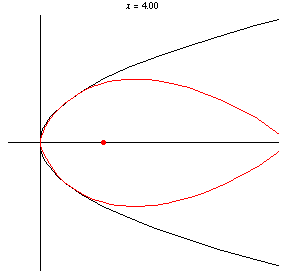
對於垂足點 
的負垂足曲線方程為
 |  | ![(at^2[a(3t^2+4)-x_0])/(at^2+x_0)](/images/equations/ParabolaNegativePedalCurve/Inline10.svg) |
(3)
|
 |  | ![-(t[a^2t^4-2a(t^2+2)x_0+x_0^2])/(at^2+x_0).](/images/equations/ParabolaNegativePedalCurve/Inline13.svg) |
(4)
|
取原點 
為垂足點，得到
 |  |  |
(5)
|
 |  |  |
(6)
|
這是一個半三次拋物線。類似地，取 
得到
 |  |  |
(7)
|
 |  |  |
(8)
|
這是一個契爾恩豪森三次曲線。
拋物線負垂足曲線
另請參閱
Negative Pedal Curve, Parabola, Parabola Pedal Curve, Tschirnhausen Cubic使用 探索
參考文獻
Ameseder, A. "Negative Fusspunktcurven der Kegelschnitte." 數學與物理文獻 64, 170-176, 1879.Lockwood, E. H. 曲線之書。 英國劍橋: Cambridge University Press, p. 157, 1967.在 中被引用
拋物線負垂足曲線請引用為
Weisstein, Eric W. "Parabola Negative Pedal Curve." 來自 —— Wolfram 網路資源。 https://mathworld.tw/ParabolaNegativePedalCurve.html