主題
Search

內擺線

下載 Mathematica 筆記本下載 Wolfram 筆記本
HypocycloidDiagram

由固定點 P 在半徑為 b 的小 圓 的 圓周 上生成，該小圓在一個半徑為 a>b 的大 圓 的內部滾動。 因此，內擺線是 外旋輪線，其中 h=b。

為了推導內擺線的方程，將小 圓 上的點繞其中心旋轉的 角度 稱為 theta，將大 圓 的中心到小 圓 的中心的 角度 稱為 phi。 則

(a-b)phi=btheta,
(1)

因此

theta=(a-b)/bphi.
(2)

稱 rho=a-2b。 如果 x(0)=rho，則第一個點在最小半徑處，內擺線的笛卡爾引數方程為

x=(a-b)cosphi-bcostheta
(3)
=(a-b)cosphi-bcos((a-b)/bphi)
(4)
y=(a-b)sinphi+bsintheta
(5)
=(a-b)sinphi+bsin((a-b)/bphi).
(6)

如果 x(0)=a，因此第一個點在最大半徑處（在 圓 上），則內擺線的方程為

x=(a-b)cosphi+bcos((a-b)/bphi)
(7)
y=(a-b)sinphi-bsin((a-b)/bphi).
(8)

內擺線的 曲率、弧長 和 切線角 由下式給出

kappa(phi)=(2b-a)/(4b(a-b))csc((aphi)/(2b))
(9)
s(phi)=(8(a-b)b)/asin^2((aphi)/(4b))
(10)
phi_t(phi)=phi(1-a/(2b)).
(11)
HypocycloidIntegers
Hypocycloids with $a/b$ an integer

一個 n 尖瓣內擺線具有 a/b=n。 對於 n=a/b 為整數且 x(0)=a，因此內擺線的方程變為

x=a/n[(n-1)cosphi-cos[(n-1)phi]
(12)
y=a/n[(n-1)sinphi+sin[(n-1)phi],
(13)

因此 弧長 和麵積為

s_n=8b(n-1)=(8a(n-1))/n
(14)
A_n=((n-1)(n-2))/(n^2)pia^2.
(15)

一個 2 尖瓣內擺線是一個 線段（Steinhaus 1999, p. 145; Kanas 2003），透過在方程 (◇) 和 (◇) 中設定 a=2b 並注意到方程簡化為

x=asinphi
(16)
y=0.
(17)

波斯天文學家和數學家納西爾丁·圖西 (Nasir Al-Din al-Tusi) (1201-1274) 注意到這一結果，有時被稱為“圖西夫婦”，以紀念他（Sotiroudis 和 Paschos 1999, p. 60; Kanas 2003）。

下表總結了對於 a/b 的特殊整數值，賦予此內擺線和其他內擺線的名稱。

n=a/b內擺線
2線段（圖西夫婦）
3三角內擺線
4星形線
HypocycloidRationals
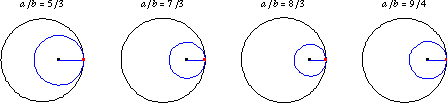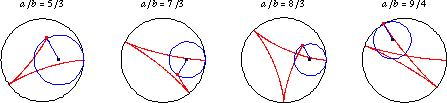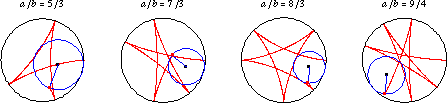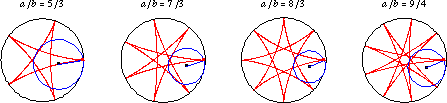
Hypocycloids with $a/b$ rational

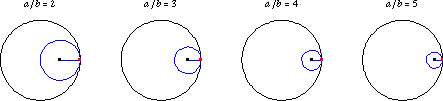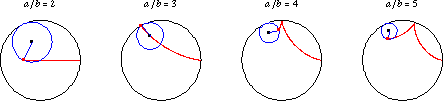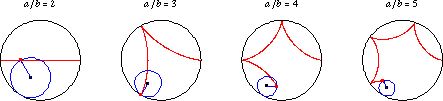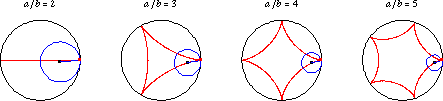
如果 n=a/b 是有理數，則曲線最終會閉合自身，並具有 a 個尖瓣。 上面說明了許多 有理數 值的 a/b 的內擺線。

HypocycloidIrrational

如果 a/b 是 無理數，則曲線永遠不會閉合自身。 上面說明了許多 無理數 值的 a/b 的內擺線。

HypocycloidConstruction

也可以透過從 圓 的 直徑 開始構造 n 尖瓣內擺線，將一端偏移一系列步長，同時將另一端在相反方向偏移 n-1 倍的步長，並延伸到 圓 的邊緣之外。 繞 圓 行駛一週後，會產生一個 n 尖瓣內擺線，如上圖所示（Madachy 1979）。

設 r 為到固定點的徑向距離。 對於 撓率半徑 rho 和 弧長 s，內擺線可以由方程給出

s^2+rho^2=16r^2
(18)

（Kreyszig 1991, pp. 63-64）。 內擺線也滿足

sin^2psi=(rho^2)/(a^2-rho^2)(a^2-r^2)/(r^2),
(19)

其中

r(dr)/(dtheta)=tanpsi
(20)

且 psi 是 半徑向量 和曲線的 切線 之間的 角度。

內擺線的方程可以寫成一種形式，這種形式在解決具有徑向對稱性的 變分法 問題時很有用。 考慮 x(0)=rho 的情況，則

r^2=x^2+y^2 =[(a-b)^2cos^2phi-2(a-b)bcosphicos((a-b)/bphi)+b^2cos^2((a-b)/bphi)+(a-b)^2sin^2phi+2(a-b)bsinphisin((a-b)/bphi)+b^2sin^2((a-b)/bphi)] ={(a-b)^2+b^2-2(a-b)b[cosphicos((a-b)/bphi)-sinphisin((a-b)/bphi)]} =(a-b)^2+b^2-2(a-b)bcos(a/bphi).
(21)

但是 rho=a-2b，所以 b=(a-rho)/2，這給出

(a-b)^2+b^2=[a-1/2(a-rho)]^2+[1/2(a-rho)]^2
(22)
=[1/2(a+rho)]^2+[1/2(a-rho)]^2
(23)
=1/2(a^2+rho^2)
(24)
2(a-b)b=2[a-1/2(a-rho)]1/2(a-rho)
(25)
=1/2(a+rho)(a-rho)
(26)
=1/2(a^2-rho^2).
(27)

現在讓

2Omegat=a/bphi,
(28)

因此

phi=(a-rho)/aOmegat
(29)
phi/(a-rho)=(Omegat)/a,
(30)

然後

r^2=1/2(a^2+rho^2)-1/2(a^2-rho^2)cos(a/bphi)
(31)
=1/2(a^2+rho^2)-1/2(a^2-rho^2)cos(2Omegat).
(32)

極角 是

tantheta=y/x=((a-b)sinphi+bsin((a-b)/aphi))/((a-b)cosphi-bcos((a-b)/aphi)).
(33)

但是

b=1/2(a-rho)
(34)
a-b=1/2(a+rho)
(35)
(a-b)/b=(a+rho)/(a-rho),
(36)

因此

tantheta=(1/2(a+rho)sinphi+1/2(a-rho)sin((a+rho)/(z-rho)phi))/(1/2(a+rho)cosphi-1/2(a-rho)cos((a+rho)/(a-rho)phi))
(37)
=((a+rho)sin((a-rho)/aOmegat)+(a-rho)sin((a+rho)/aOmegat))/((a+rho)cos((a-rho)/aOmegat)-(a-rho)cos((a+rho)/aOmegat))
(38)
=(a[sin((a-rho)/aOmegat)+sin((a+rho)/aOmegat)]+rho[sin((a-rho)/aOmegat)-sin((a+rho)/aOmegat)])/(a[cos((a-rho)/aOmegat)-cos((a+rho)/aOmegat)]+rho[cos((a-rho)/aOmegat)+cos((a+rho)/aOmegat)])
(39)
=(2asin(Omegat)cos(rho/aOmegat)-2rhocos(Omegat)sin(rho/aOmegat))/(2asin(Omegat)sin(rho/aOmegat)+2rhocos(Omegat)cos(rho/aOmegat))
(40)
=(atan(Omegat)-rhotan(rho/aOmegat))/(atan(Omegat)tan(rho/aOmegat)+rho).
(41)

計算

tan(theta+rho/aOmegat)=([atan(Omegat)-rhotan(rho/aOmegat)+tan(rho/aOmegat)][atan(Omegat)tan(rho/aOmegat)+rho])/([atan(Omegat)tan(rho/aOmegat)+rho]-[atan(Omegat)-rhotan(rho/aOmegat)]tan(rho/aOmegat))
(42)
=(atan(Omegat)[1+tan^2(rho/aOmegat)])/(rho[1+tan^2(rho/aOmegat)])
(43)
=a/rhotan(Omegat),
(44)

然後給出

theta=tan^(-1)[a/rhotan(Omegat)]-rho/aOmegat.
(45)

最後，代入得到

theta=tan^(-1)[a/rhotan(a/(a-rho)phi)]-rho/aa/(a-rho)phi
(46)
=tan^(-1)[a/rhotan(a/(a-rho)phi)]-rho/(a-rho)phi.
(47)

這種形式在解決 帶隧道的球體 問題時很有用，這是 最速降線問題 的推廣，目的是找到在重力場中穿過 球體（重力根據高斯定律變化）的隧道的形狀，使得在重力作用下，球體 表面上兩點之間的旅行時間最小化。

另請參閱

星形線, 旋輪線, 三角內擺線, 外擺線, 內擺線漸屈線, 內擺線漸伸線, 內擺線垂足曲線, 圖西夫婦

使用 探索

參考文獻

Bogomolny, A. "Cycloids." http://www.cut-the-knot.org/pythagoras/cycloids.shtml.Borwein, J. 和 Bailey, D. 實驗數學：21 世紀的合理推理。 Wellesley, MA: A K Peters, p. 83, 2003.Kanas, N. "From Ptolemy to the Renaissance: How Classical Astronomy Survived the Dark Ages." 天空與望遠鏡 105, 50-58, 1 月 2003.Kreyszig, E. 微分幾何。 New York: Dover, 1991.Lawrence, J. D. 特殊平面曲線目錄。 New York: Dover, pp. 171-173, 1972.Lemaire, J. Hypocycloïdes et epicycloïdes. Paris: Albert Blanchard, 1967.MacTutor 數學史檔案館. "Hypocycloid." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hypocycloid.html.Madachy, J. S. Madachy 的數學娛樂。 New York: Dover, pp. 225-231, 1979.Sotiroudis, P. 和 Paschos, E. A. 星圖：公元 1300 年以來的拜占庭天文學。 Singapore: World Scientific, 1999.Steinhaus, H. 數學快照，第 3 版。 New York: Dover, 1999.Wagon, S. Mathematica 實戰。 New York: W. H. Freeman, pp. 50-52, 1991.Yates, R. C. "Epi- and Hypo-Cycloids." 曲線及其性質手冊。 Ann Arbor, MI: J. W. Edwards, pp. 81-85, 1952.

請引用本文為

Weisstein, Eric W. "內擺線。" 來自 Web 資源。 https://mathworld.tw/Hypocycloid.html

學科分類