主題
Search

第一類貝塞爾函式

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
BesselJ

第一類貝塞爾函式 J_n(x) 被定義為 貝塞爾微分方程 的解

x^2(d^2y)/(dx^2)+x(dy)/(dx)+(x^2-n^2)y=0
(1)

這些解在原點處是非奇異的。它們有時也被稱為柱函式或柱諧函式。 上圖顯示了 J_n(x)，當 n=0, 1, 2, ..., 5 時。 符號 J_(z,n) 最初由 Hansen (1843) 使用，隨後 Schlömilch (1857) 也使用該符號來表示現在寫作的 J_n(2z) (Watson 1966, p. 14)。 然而，Hansen 對函式本身的定義，以 生成函式 的形式給出

e^(z(t-1/t)/2)=sum_(n=-infty)^inftyt^nJ_n(z).
(2)

與現代定義相同 (Watson 1966, p. 14)。 貝塞爾使用符號 I_k^h 來表示現在稱為第一類貝塞爾函式的函式 (Cajori 1993, vol. 2, p. 279)。

貝塞爾函式 J_n(z) 也可以透過 輪廓積分 定義

J_n(z)=1/(2pii)∮e^((z/2)(t-1/t))t^(-n-1)dt,
(3)

其中輪廓包圍原點，並沿逆時針方向遍歷 (Arfken 1985, p. 416)。

第一類貝塞爾函式在 Wolfram 語言 中實現為BesselJ[ν, z]。

為了求解微分方程，應用 弗羅貝尼烏斯方法，使用 形式為 的級數解

y=x^ksum_(n=0)^inftya_nx^n=sum_(n=0)^inftya_nx^(n+k).
(4)

代入 (1) 得到

x^2sum_(n=0)^infty(k+n)(k+n-1)a_nx^(k+n-2)+xsum_(n=0)^infty(k+n)a_nx^(k+n-1)+x^2sum_(n=0)^inftya_nx^(k+n)-m^2sum_(n=0)^inftya_nx^(n+k)=0
(5)
sum_(n=0)^infty(k+n)(k+n-1)a_nx^(k+n)+sum_(n=0)^infty(k+n)a_nx^(k+n) +sum_(n=2)^inftya_(n-2)x^(k+n)-m^2sum_(n=0)^inftya_nx^(n+k)=0.
(6)

指標方程，透過設定 n=0 獲得，為

a_0[k(k-1)+k-m^2]=a_0(k^2-m^2)=0.
(7)

由於 a_0 被定義為第一個 非零 項，k^2-m^2=0，所以 k=+/-m。現在，如果 k=m,

sum_(n=0)^infty[(m+n)(m+n-1)+(m+n)-m^2]a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0
(8)
sum_(n=0)^infty[(m+n)^2-m^2]a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0
(9)
sum_(n=0)^inftyn(2m+n)a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0
(10)
a_1(2m+1)x^(m+1)+sum_(n=2)^infty[a_nn(2m+n)+a_(n-2)]x^(m+n)=0.
(11)

首先，檢視特殊情況 m=-1/2，那麼 (11) 變為

sum_(n=2)^infty[a_nn(n-1)+a_(n-2)]x^(m+n)=0,
(12)

所以

a_n=-1/(n(n-1))a_(n-2).
(13)

現在令 n=2l，其中 l=1, 2, ....

a_(2l)=-1/(2l(2l-1))a_(2l-2)
(14)
=((-1)^l)/([2l(2l-1)][2(l-1)(2l-3)]...[2·1·1])a_0
(15)
=((-1)^l)/(2^ll!(2l-1)!!)a_0,
(16)

它使用恆等式 2^ll!(2l-1)!!=(2l)!，給出

a_(2l)=((-1)^l)/((2l)!)a_0.
(17)

類似地，令 n=2l+1,

a_(2l+1)=-1/((2l+1)(2l))a_(2l-1)=((-1)^l)/([2l(2l+1)][2(l-1)(2l-1)]...[2·1·3][1])a_1,
(18)

它使用恆等式 2^ll!(2l+1)!!=(2l+1)!，給出

a_(2l+1)=((-1)^l)/(2^ll!(2l+1)!!)a_1=((-1)^l)/((2l+1)!)a_1.
(19)

代回到 (◇) 中，當 k=m=-1/2 時，得到

y=x^(-1/2)sum_(n=0)^(infty)a_nx^n
(20)
=x^(-1/2)[sum_(n=1,3,5,...)^(infty)a_nx^n+sum_(n=0,2,4,...)^(infty)a_nx^n]
(21)
=x^(-1/2)[sum_(l=0)^(infty)a_(2l)x^(2l)+sum_(l=0)^(infty)a_(2l+1)x^(2l+1)]
(22)
=x^(-1/2)[a_0sum_(l=0)^(infty)((-1)^l)/((2l)!)x^(2l)+a_1sum_(l=0)^(infty)((-1)^l)/((2l+1)!)x^(2l+1)]
(23)
=x^(-1/2)(a_0cosx+a_1sinx).
(24)

階數為 +/-1/2 的 貝塞爾函式 因此被定義為

J_(-1/2)(x)=sqrt(2/(pix))cosx
(25)
J_(1/2)(x)=sqrt(2/(pix))sinx,
(26)

所以 m=+/-1/2 的通解為

y=a_0^'J_(-1/2)(x)+a_1^'J_(1/2)(x).
(27)

現在，考慮一般情況 m!=-1/2。方程 (◇) 要求

a_1(2m+1)=0
(28)
[a_nn(2m+n)+a_(n-2)]x^(m+n)=0
(29)

對於 n=2, 3, ..., 所以

a_1=0
(30)
a_n=-1/(n(2m+n))a_(n-2)
(31)

對於 n=2, 3, .... 令 n=2l+1，其中 l=1, 2, ..., 那麼

a_(2l+1)=-1/((2l+1)[2(m+l)+1])a_(2l-1)
(32)
=...=f(n,m)a_1=0,
(33)

其中 f(n,m) 是 l 和 m 的函式，透過迭代遞迴關係到 a_1 獲得。現在令 n=2l，其中 l=1, 2, ..., 所以

a_(2l)=-1/(2l(2m+2l))a_(2l-2)
(34)
=-1/(4l(m+l))a_(2l-2)
(35)
=((-1)^l)/([4l(m+l)][4(l-1)(m+l-1)]...[4·(m+1)])a_0.
(36)

代回到 (◇) 中，

y=sum_(n=0)^(infty)a_nx^(n+m)=sum_(n=1,3,5,...)^(infty)a_nx^(n+m)+sum_(n=0,2,4,...)^(infty)a_nx^(n+m)
(37)
=sum_(l=0)^(infty)a_(2l+1)x^(2l+m+1)+sum_(l=0)^(infty)a_(2l)x^(2l+m)
(38)
=a_0sum_(l=0)^(infty)((-1)^l)/([4l(m+l)][4(l-1)(m+l-1)]...[4(m+1)])x^(2l+m)
(39)
=a_0sum_(l=0)^(infty)([(-1)^lm(m-1)...1]x^(2l+m))/([4l(m+l)][4(l-1)(m+l-1)]...[4(m+1)m...1])
(40)
=a_0sum_(l=0)^(infty)((-1)^lm!)/(2^(2l)l!(m+l)!)x^(2l+m).
(41)

現在定義

J_m(x)=sum_(l=0)^infty((-1)^l)/(2^(2l+m)l!(m+l)!)x^(2l+m),
(42)

其中階乘可以推廣到非整數 m 的 伽瑪函式。上面的方程變為

y=a_02^mm!J_m(x)=a_0^'J_m(x).
(43)

回到方程 (◇) 並檢查情況 k=-m,

a_1(1-2m)+sum_(n=2)^infty[a_nn(n-2m)+a_(n-2)]x^(n-m)=0.
(44)

然而，m 的符號是任意的，因此對於 +m 和 -m，解必須相同。因此，我們可以自由地用 -|m| 替換 -m，所以

a_1(1+2|m|)+sum_(n=2)^infty[a_nn(n+2|m|)+a_(n-2)]x^(|m|+n)=0,
(45)

我們得到與之前相同的解，但 m 被 |m| 替換。

J_m(x)={sum_(l=0)^(infty)((-1)^l)/(2^(2l+|m|)l!(|m|+l)!)x^(2l+|m|) for |m|!=1/2; sqrt(2/(pix))cosx for m=-1/2; sqrt(2/(pix))sinx for m=1/2.
(46)

我們可以透過寫入以下公式來關聯 J_m(x) 和 J_(-m)(x) (當 m 是一個 整數 時)

J_(-m)(x)=sum_(l=0)^infty((-1)^l)/(2^(2l-m)l!(l-m)!)x^(2l-m).
(47)

現在令 l=l^'+m。那麼

J_(-m)(x)=sum_(l^'+m=0)^(infty)((-1)^(l^'+m))/(2^(2l^'+m)(l^'+m)!l!)x^(2l^'+m)
(48)
=sum_(l^'=-m)^(-1)((-1)^(l^'+m))/(2^(2l^'+m)l^'!(l^'+m)!)x^(2l^'+m)+sum_(l^'=0)^(infty)((-1)^(l^'+m))/(2^(2l^'+m)l^'!(l^'+m)!)x^(2l^'+m).
(49)

但是對於 l^'=-m,...,-1，l^'!=infty，所以 分母 是無窮大，左側的項為零。因此我們有

J_(-m)(x)=sum_(l=0)^(infty)((-1)^(l+m))/(2^(2l+m)l!(l+m)!)x^(2l+m)
(50)
=(-1)^mJ_m(x).
(51)

請注意，貝塞爾微分方程 是 二階 的，因此必須有兩個線性獨立的解。我們只為 |m|=1/2 找到了兩個解。對於一般的非整數階，獨立的解是 J_m 和 J_(-m)。當 m 是一個 整數 時，通解（實數解）是 形式為

Z_m=C_1J_m(x)+C_2Y_m(x),
(52)

其中 J_m 是第一類貝塞爾函式，Y_m (又名 N_m) 是 第二類貝塞爾函式 (又名諾伊曼函式或韋伯函式)，C_1 和 C_2 是常數。複數解由 漢克爾函式 (又名第三類貝塞爾函式) 給出。

貝塞爾函式在 [0,a] 中是 正交的，根據

int_0^aJ_nu(alpha_(num)rho/a)J_nu(alpha_(nun)rho/a)rhodrho=1/2a^2[J_(nu+1)(alpha_(num))]^2delta_(mn),
(53)

其中 alpha_(num) 是 mth 個 Jnu 零點，delta_(mn) 是 克羅內克 delta (Arfken 1985, p. 592)。

除非 2m 是一個 負整數，

J_m(z)=(z^(-1/2))/(2^(2m+1/2)i^(m+1/2)Gamma(m+1))M_(0,m)(2iz),
(54)

其中 Gamma(x) 是 伽瑪函式，M_(0,m) 是一個 惠特克函式。

用 第一類合流超幾何函式 表示，貝塞爾函式寫為

J_nu(z)=((1/2z)^nu)/(Gamma(nu+1))_0F_1(nu+1;-1/4z^2).
(55)

一個用於用 J_0(z) 表示更高階貝塞爾函式的導數恆等式是

J_n(z)=i^nT_n(id/(dz))J_0(z),
(56)

其中 T_n(z) 是 第一類切比雪夫多項式。貝塞爾函式的漸近形式為

J_m(z) approx 1/(Gamma(m+1))(z/2)^m
(57)

對於 z<<1 和

J_m(z) approx sqrt(2/(piz))cos(z-(mpi)/2-pi/4)
(58)

對於 z>>|m^2-1/4| (修正了 Abramowitz 和 Stegun 1972, p. 364 的條件)。

一個導數恆等式是

d/(dx)[x^mJ_m(x)]=x^mJ_(m-1)(x).
(59)

一個積分恆等式是

int_0^uu^'J_0(u^')du^'=uJ_1(u).
(60)

一些求和恆等式是

sum_(k=-infty)^inftyJ_k(x)=1
(61)

(這從生成函式 (◇) 和 t=1 得出),

1=[J_0(x)]^2+2sum_(k=1)^infty[J_k(x)]^2
(62)

(Abramowitz 和 Stegun 1972, p. 363),

1=J_0(x)+2sum_(k=1)^inftyJ_(2k)(x)
(63)

(Abramowitz 和 Stegun 1972, p. 361),

0=sum_(k=0)^(2n)(-1)^kJ_k(z)J_(2n-k)(z)+2sum_(k=1)^inftyJ_k(z)J_(2n+k)(z)
(64)

對於 n>=1 (Abramowitz 和 Stegun 1972, p. 361),

J_n(2z)=sum_(k=0)^nJ_k(z)J_(n-k)(z)+2sum_(k=1)^infty(-1)^kJ_k(z)J_(n+k)(z)
(65)

(Abramowitz 和 Stegun 1972, p. 361), 和 雅可比-安格爾展開

e^(izcostheta)=sum_(n=-infty)^inftyi^nJ_n(z)e^(intheta),
(66)

也可以寫成

e^(izcostheta)=J_0(z)+2sum_(n=1)^inftyi^nJ_n(z)cos(ntheta).
(67)

貝塞爾函式加法定理指出

J_n(y+z)=sum_(m=-infty)^inftyJ_m(y)J_(n-m)(z).
(68)

各種積分可以用貝塞爾函式表示

J_n(z)=1/piint_0^picos(zsintheta-ntheta)dtheta,
(69)

這是 貝塞爾第一積分,

J_n(z)=(i^(-n))/piint_0^pie^(izcostheta)cos(ntheta)dtheta
(70)
J_n(z)=1/(2pii^n)int_0^(2pi)e^(izcosphi)e^(inphi)dphi
(71)

對於 n=1, 2, ...,

J_n(z)=2/pi(z^n)/((2n-1)!!)int_0^(pi/2)sin^(2n)ucos(zcosu)du
(72)

對於 n=1, 2, ...,

J_n(x)=1/(2pii)int_gammae^((x/2)(z-1/z))z^(-n-1)dz
(73)

對於 n>-1/2。貝塞爾函式被歸一化，使得

int_0^inftyJ_n(x)dx=1
(74)

對於正整數（和實數） n。涉及 J_1(x) 的積分包括

int_0^infty[(J_1(x))/x]^2dx=4/(3pi)
(75)
int_0^infty[(J_1(x))/x]^2xdx=1/2.
(76)

第一類貝塞爾函式的比率具有 連分數

(J_(n-1)(z))/(J_n(z))=(2n)/z-(z/(2(n+1)))/(1-(((z/2)^2)/((n+1)(n+2)))/((1-((z/2)^2)/((n+2)(n+3)))/(1-...)))
(77)

(Wall 1948, p. 349)。

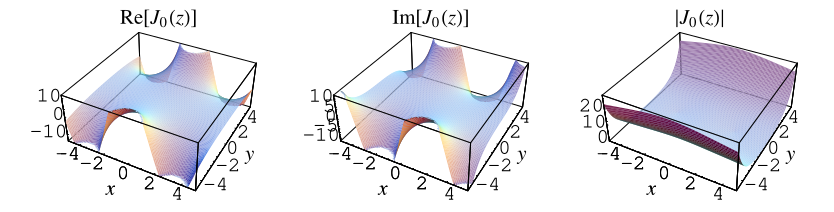
BesselJ0ReIm
BesselJ0Contours

特殊情況 n=0 給出 J_0(z) 作為級數

J_0(z)=sum_(k=0)^infty(-1)^k((1/4z^2)^k)/((k!)^2)
(78)

(Abramowitz 和 Stegun 1972, p. 360), 或積分

J_0(z)=1/piint_0^pie^(izcostheta)dtheta.
(79)

參見

第二類貝塞爾函式, 貝塞爾函式零點, 德拜漸近表示, 狄克遜-費拉公式, 漢森-貝塞爾公式, 卡普坦級數, 克內澤爾-索末菲公式, 梅勒貝塞爾函式公式, 第一類修正貝塞爾函式, 第二類修正貝塞爾函式, 尼科爾森公式, 泊松貝塞爾函式公式, 瑞利函式, 施萊夫利公式, 施勒米爾希級數, 索末菲公式, 索寧-沙夫海特林公式, 沃森公式, 沃森-尼科爾森公式, 韋伯不連續積分, 韋伯公式, 韋伯-索寧公式, 韋裡希公式 在 課堂中探索此主題

相關 Wolfram 網站

http://functions.wolfram.com/Bessel-TypeFunctions/BesselJ/

在 中探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (編). "貝塞爾函式 J 和 Y." §9.1 in 數學函式手冊，包含公式、圖表和數學表格，第 9 次印刷。 紐約: Dover, pp. 358-364, 1972.Arfken, G. "第一類貝塞爾函式，J_nu(x)" 和 "正交性." §11.1 和 11.2 in 物理學家數學方法，第 3 版。 奧蘭多, FL: Academic Press, pp. 573-591 和 591-596, 1985.Cajori, F. 數學符號史，第 1-2 卷。 紐約: Dover, 1993.Hansen, P. A. "確定任意偏心率和傾角橢圓中的絕對擾動，I." Schriften der Sternwarte Seeberg. 哥達, 1843.Lehmer, D. H. "貝塞爾函式的算術週期性." 數學年刊 33, 143-150, 1932.Le Lionnais, F. Les nombres remarquables. 巴黎: Hermann, 1983.Morse, P. M. 和 Feshbach, H. 理論物理方法，第一部分。 紐約: McGraw-Hill, pp. 619-622, 1953.Schlömilch, O. X. "關於貝塞爾函式." Z. für Math. u. Phys. 2, 137-165, 1857.Spanier, J. 和 Oldham, K. B. "貝塞爾係數 J_0(x) 和 J_1(x)" 和 "貝塞爾函式 J_nu(x)." 第 52-53 章 in 函式圖集。 華盛頓特區: Hemisphere, pp. 509-520 和 521-532, 1987.Wall, H. S. 連分數解析理論。 紐約: Chelsea, 1948.Watson, G. N. 貝塞爾函數理論專著，第 2 版。 劍橋，英格蘭: 劍橋大學出版社, 1966.

在 上被引用

第一類貝塞爾函式

請引用為

Weisstein, Eric W. "第一類貝塞爾函式." 來自 Web 資源. https://mathworld.tw/BesselFunctionoftheFirstKind.html

學科分類