增廣是截斷的對偶操作,它用高度為 (其中
可以是正數、零或負數)的稜錐替換多面體的面(Cromwell 1997,第 124 頁和 195-197 頁)。該操作有時也稱為堆積、akisation(因為它將正多邊形轉換為
-akis 多面體,即,面數變為四倍)、加帽或累積。
B. Grünbaum 使用術語 elevatum 和 invaginatum 分別表示增廣中使用的正高度(向外指向)和負高度(向內指向)稜錐。
術語“增廣”有時也用於更廣泛的上下文中,指在一個基本立體的面上附加一個多面體帽。一個例子是稱為增廣截角立方體的約翰遜多面體,其中附加的形狀是正方形圓頂——而不是稜錐。
增廣在錯誤的名稱下實現Stellate[poly, ratio] 在 Wolfram 語言 包中PolyhedronOperations`並在 Wolfram 語言 中實現為AugmentedPolyhedron[poly]。
礦物學家給出了規則立體的增廣形式的以下特殊名稱(Berry 和 Mason 1959,第 124 頁和 127 頁)。
使用 進行增廣給出了原始立體的三角剖分版本。下圖說明了從負到正增廣高度的 柏拉圖立體 的增廣系列。
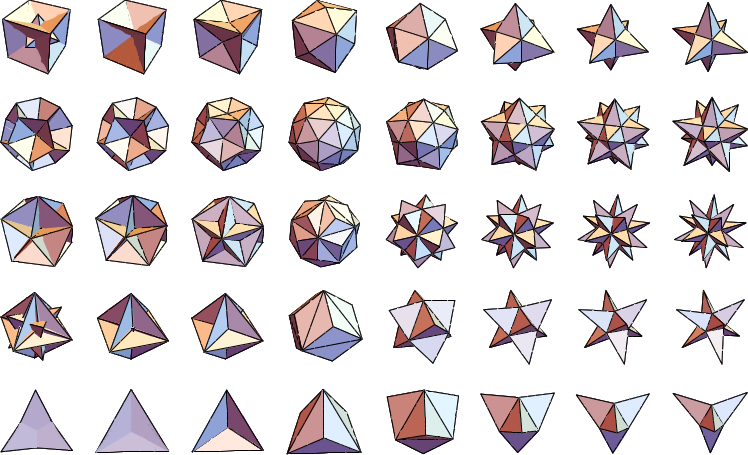
下圖和表格給出了在邊長為單位的 柏拉圖立體 上透過給定高度的增廣形成的特殊立體。
| 原始 | 增廣 | |
| 立方體 | 四角六面體 | |
| 立方體 | 菱形十二面體 | |
| 立方體 | 星形 等邊 24-三角面體 | |
| 正十二面體 | 五角十二面體 | |
| 正十二面體 | 星形 等邊 60-三角面體 | |
| 正十二面體 | 小星形十二面體 | |
| 正二十面體 | 大十二面體 | |
| 正二十面體 | 小三方二十面體 | |
| 正二十面體 | 星形 等邊 60-三角面體 | |
| 正二十面體 | 大星形十二面體 | |
| 正八面體 | 小三方八面體 | |
| 正八面體 | 星狀八面體 | |
| 正四面體 | 三方四面體 | |
| 正四面體 | 立方體 | |
| 正四面體 | 星形 等邊 12-三角面體 |

|

|

|

|
上面的頂部影像顯示了一個摺紙增廣四面體和增廣十二面體。 它們使用三角形邊緣模組構建,並以類似於 Gurkewitz 和 Arnstein (1995, p. 53) 描述的其他實體的方式構建。 左下方的圖顯示了一個向內增廣的十二面體(Fusè 1990,pp. 126-129),對應於 二十面體星狀體 (number 26) in Coxeter et al. (1999, pp. 43 and 64),而右圖顯示了 E. W. Weisstein 構建的增廣二十面體(Kasahara 和 Takahama 1987,p. 45)。