小三八面體

通常，三八面體是非正規的二十四面體，可以構造為正八面體的正增廣。這種立體也稱為三方八面體，尤其是在礦物學家中（Correns 1949，第41頁；Berry and Mason 1959，第127頁）。雖然由此產生的二十四面體不是正規的，但其面都是相同的。

製作您自己的小三八面體

列印並摺疊

3D 列印

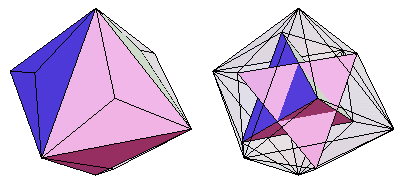
小三八面體，被 Holden (1971, p. 55) 簡稱為三八面體，是截角立方體的24面對偶多面體，也是 Wenninger 對偶 。新增“小”字是為了將其與大三八面體區分開來，後者是星形截角六面體的對偶。上面展示了它，以及線框版本和一個可用於其構造的網格。

小三八面體可以透過單位邊長的八面體的增廣來構造，增廣的稜錐高度為 。

小三八面體出現在 M. C. Escher 1948 年的木刻版畫“星星”的中間右側，作為多面體“星星”之一（Forty 2003，圖版 43）。

它在 Wolfram 語言中實現為PolyhedronData["SmallTriakisOctahedron"].

小三八面體是等邊增廣立方體的凸包。

八面體和星形八面體可以內接在小三八面體的頂點上（E. Weisstein，2009 年 12 月 25 日）。

小三八面體的對偶多面體是截角立方體，兩者都與它們的公共中球一起在上面展示。對於單位邊長的截角立方體，其對偶的邊長為

			(1)
			(2)

歸一化使得 ，得到的小三八面體的表面積和體積為

			(3)
			(4)