(第一)菱形十二面體是 立方八面體 的 對偶多面體 (Holden 1971, p. 55)。它有時也被稱為菱面體十二面體 (Cotton 1990),並且在需要將其與 Bilinski 十二面體 (Bilinski 1960, Chilton and Coxeter 1963) 區分開來時,可能會包含“第一”。上面展示了它的圖形,以及線框版本和一個可用於其構建的 網格。
它是 Wenninger 對偶 。
菱形十二面體在 Wolfram 語言 中實現為PolyhedronData["RhombicDodecahedron"].
菱形十二面體出現在右上角,作為 M. C. Escher 1948 年木刻版畫“星星” (Forty 2003, Plate 43) 中的多面體“星星”之一。
菱形十二面體的 14 個頂點由 12 個 菱形 連線而成,尺寸如下圖所示,其中
|
(1)
| |||
|
(2)
| |||
|
(3)
| |||
|
(4)
| |||
|
(5)
|
|
|
|
|
菱形十二面體可以透過在一箇中心立方體的面上放置六個立方體,以金屬“傑克”的配置(左圖)構建而成。然後,將外部立方體的中心與中心立方體的頂點連線起來,即可得到菱形十二面體(中圖)。在邊長為單位長度的 立方體 的每個面上貼上高度為 1/2 的 正方錐體,即可得到菱形十二面體(右圖;Brückner 1900, p. 130;Steinhaus 1999, p. 185)。
連線菱形十二面體的長對角線(上圖中藍色所示)會得到 八面體 的邊,而短對角線則會得到 立方體 的邊(紅色)。
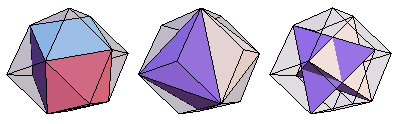
更具體地說,立方體、八面體 和 星形八面體 可以內接於菱形十二面體的頂點 (E. Weisstein, Dec. 25, 2009)。
菱形十二面體是 立方體-八面體複合體 和第一個 立方八面體星狀體 的 凸包。
如果菱形十二面體沿著三個連續的面對角線鉸接成六個正方錐體,則所得模型可以摺疊成一個立方體 (Wells 1991)。菱形十二面體的一種可能的構造稱為 Bauspiel。它也可以透過將單位邊長的 立方體 增廣 一個高度為 1/2 的錐體來構造。
菱形十二面體是 帶狀多面體 和 空間填充多面體 (Steinhaus 1999, p. 185)。頂點由 (,
,
), (
, 0, 0), (0,
, 0), (0, 0,
) 給出。
|
|
|
在上面繪製的點中 相交 的 立方體-八面體複合體 的邊是 菱形 的對角線(左圖),而 12 個 菱形 形成菱形十二面體(中心圖;Ball 和 Coxeter 1987)。立方八面體 可以內接於菱形十二面體(右圖;Steinhaus 1999, p. 206)。
菱形十二面體有三種星狀體。

菱形十二面體可以使用 Haűy 構造 構建。Haűy 菱形十二面體數
|
(6)
|
給出了一種計算菱形十二面體 體積 的方法,
 |
(7)
| ||
|
(8)
|
(Steinhaus 1999)。單位邊長的菱形十二面體的 表面積 為
|
(9)
|
其慣性張量為
![I=[1/3Ma^2 0 0; 0 1/3Ma^2 0; 0 0 1/3Ma^2].](/images/equations/RhombicDodecahedron/NumberedEquation3.svg) |
(10)
|
