Zonohedron

考慮空間中穿過一點的任意 個線段的星形，使得沒有三條線共面。那麼存在一個多面體，稱為 zonohedron，其面由 個菱形組成，並且其邊與給定的 條線平行，每組 條邊平行於一條線。此外，對於每對 條線，都有一對相對的面，其邊位於這些方向上 (Ball and Coxeter 1987, p. 141)。因此，zonohedron 是一種每個面都是中心對稱的多面體 (Towle 1996, Eppstein)。

關於 zonotope 的定義存在一些混淆 (Eppstein 1996)。Wells (1991, pp. 274-275) 要求生成向量處於一般位置（所有 -元組的向量必須張成整個空間），以便 zonotope 的所有面都是平行多面體。其他人（Bern et al. 1995；Ziegler 1995, pp. 198-208；Eppstein 1996）沒有做此限制。Coxeter (1973) 從一個定義開始，但很快切換到另一個定義。

雖然所有 zonohedra 的 Dehn 不變數都為 0，但只有作為 平行多面體Paralleohedron 的 zonohedra 才是空間填充的。

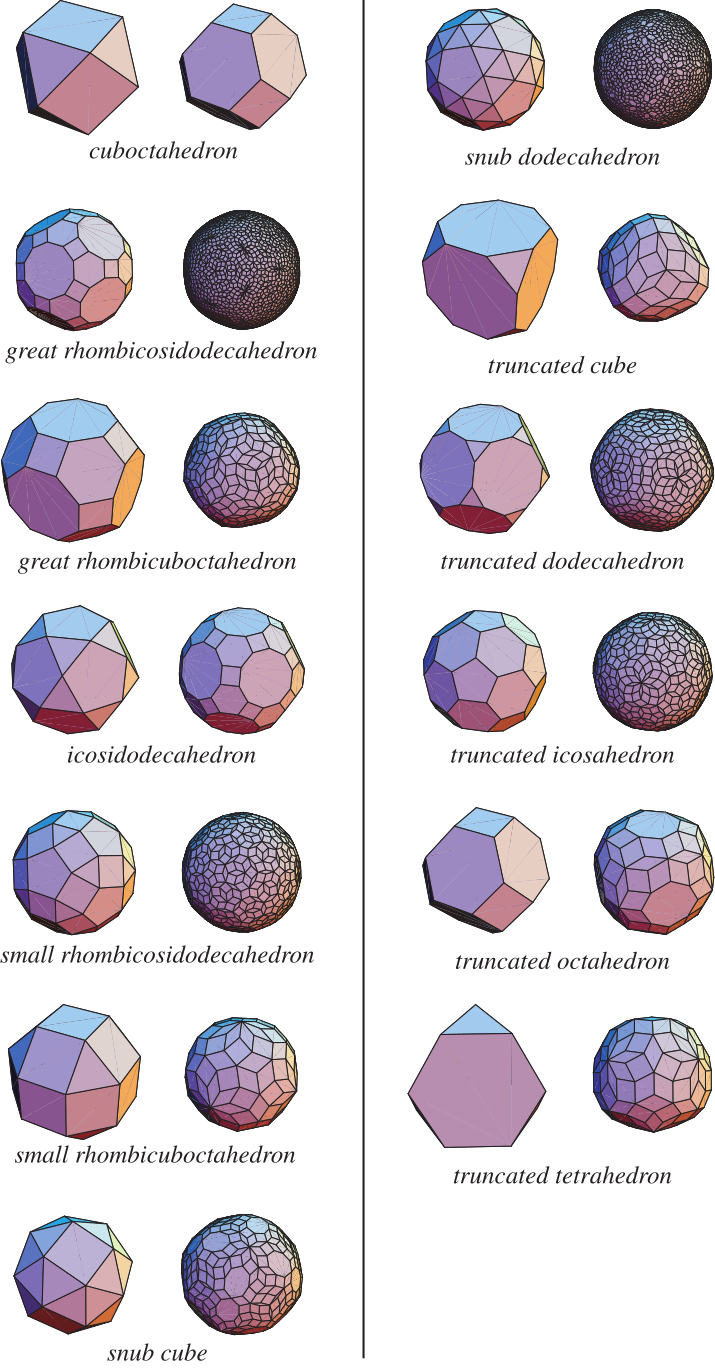
上面的圖示說明了阿基米德立體以及由其非平行頂點確定的 zonohedra。

類似地，上面的圖示說明了柏拉圖立體以及由其非反平行頂點子集確定的 zonohedra。

zonohedron 面的組合數學等同於平面中直線排列的組合數學 (Eppstein 1996)。

如果線段都具有相等的長度，則 zonohedron 被稱為等邊 zonohedron (Coxeter 1973, p. 29)。

在一個非奇異 zonohedron 中存在 個平行四邊形，其中 是多面體邊出現的不同方向的數量 (Ball and Coxeter 1987, pp. 141-144)。

每個僅由平行四邊形界定的凸多面體都是 zonohedron (Coxeter 1973, p. 27)，每個面是平行邊 -邊形的凸多面體也是 zonohedron (Coxeter 1973, p. 29)

除了等邊和極座標 zonohedra 之外，平行六面體、主平行多面體 (Coxeter 1973, pp. 29-30) 和菱面體也是 zonohedra。