正交群

對於每個維度 ，正交群 是 正交矩陣的群。這些矩陣構成一個群，因為它們在乘法和取逆運算下是封閉的。

將矩陣視為由 座標函式給出，矩陣集合等同於 。正交矩陣是 個方程的解

(1)

其中 是單位矩陣，這些方程是冗餘的。其中只有 個是獨立的，剩下 個“自由變數”。實際上，正交群是一個光滑的 維子流形。

由於正交群是群和流形，因此它是李群。 在單位元處有一個子流形切空間，它是反對稱矩陣 的李代數。實際上，正交群是一個緊李群。

行列式一個正交矩陣的行列式為 1 或 ，因此正交群有兩個連通分支。包含單位元的連通分支是特殊正交群 。例如，群 在平面上的群作用是旋轉

(2)

其中 是 中的任意實數。這些矩陣保持二次形式 不變，因此它們也保持圓 不變，這些圓是群軌道。

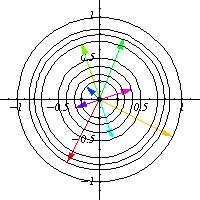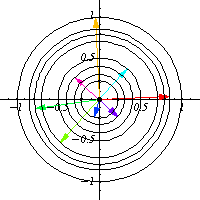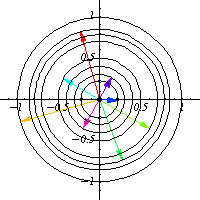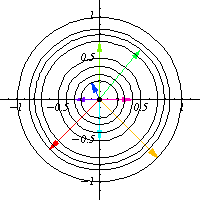
作為流形， 由圓的兩個不相交的副本組成。

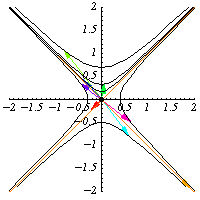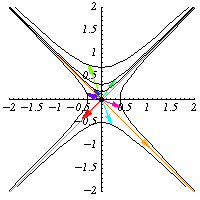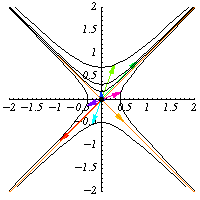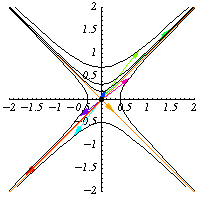
正交群有幾種推廣。首先，可以為任何具有矩陣簽名 的對稱二次型 定義正交群。保持 不變的矩陣 的群，即，

(3)

被記為 。洛倫茲群是 。例如，矩陣

(4)

是 的元素。它們保持二次形式 不變，因此它們保持雙曲線 不變。

除了使用實數作為係數，還可以使用來自任何域 的係數，在這種情況下，它被記為 。正交矩陣仍然滿足 。例如， 包含

(5)

並且總共有 48 個元素。

當然， 表示保持具有矩陣簽名 的對稱二次型的矩陣群，其係數在域 中。當 不是 或 時，這些群被稱為李型群。

當係數是複數時，它被稱為復正交群，它與酉群非常不同。例如，形式為

(6)

的矩陣在 中。特別地， 不是緊李群。在仿射空間中定義 的方程是二次多項式。因此， 是線性代數群。

正交群 中階數為 , 2, 3, ... 的子群數量 是 1, 3, 1, 5, 1, 5, 1, 7, 1, 5, 1, 8, ... (OEIS A001051)，即 {1,5,1,7} 的重複序列，例外情況為 , , , , 以及 。