主題
Search

Sinc 函式

下載 Mathematica Notebook下載 Wolfram Notebook
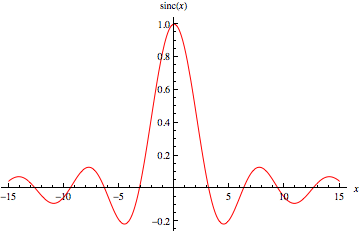
SincReal
最小值 最大值
Powered by webMathematica

sinc 函式 sinc(x)，也稱為“取樣函式”，是在訊號處理和 傅立葉變換 理論中經常出現的一個函式。該函式的全稱是“sine cardinal”，但通常以其縮寫“sinc”來稱呼。通常使用兩種定義。本文采用的定義是

sinc(x)={1 for x=0; (sinx)/x otherwise,
(1)

其中 sinx 是 正弦 函式，如上圖所示。

這具有歸一化

int_(-infty)^inftysinc(x)dx=pi.
(2)

此函式在 Wolfram 語言 中實現為Sinc[x]。

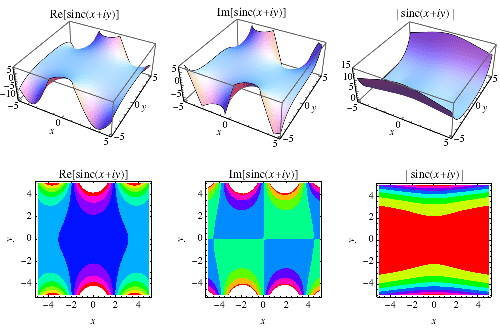SincReImAbs
最小值 最大值
Re
Im Powered by webMathematica

當擴充套件到 複平面 時，sinc(z) 如上圖所示。

SincCos

關於 sinc(x) 的一個有趣的性質是，sinc(x) 的 區域性極值 集合對應於其與 餘弦 函式 cos(x) 的交點，如上圖所示。

導數 由下式給出

(dsinc(z))/(dz)=(cosz)/z-(sinz)/(z^2)
(3)

不定積分 由下式給出

intsinc(z)dz=Si(z),
(4)

其中 Si(z) 是 正弦積分。

Woodward (1953)、McNamee et al. (1971) 和 Bracewell (1999, p. 62) 採用了另一種定義

sinc_pi(x)=sinc(pix)
(5)
={1 for x=0; (sin(pix))/(pix) otherwise.
(6)

後一種定義有時更方便，因為它具有簡單的歸一化，

int_(-infty)^inftysinc_pi(x)dx=1.
(7)

該變體也滿足求和式

sum_(k=-infty)^inftysinc(pik)=1.
(8)

此外，二項式係數 滿足

(0; x)=sinc_(pi)(x),
(9)

這本質上是 反射關係 的重述

Gamma(1+x)Gamma(1-x)=(pix)/(sin(pix))=1/(sinc_(pi)(x))
(10)

伽瑪函式 的反射關係 (M. Somos, 私人通訊，2006 年 10 月 26 日)。

sinc 函式與 第一類球貝塞爾函式 j_n(x) 密切相關，特別是

sinc(x)=j_0(x),
(11)

並且用 Meijer G-函式 表示為

sinc(z)=(sqrt(pi))/2G_(02)^(10)(1/2z,1/2|-; 0,1/2).
(12)

設 Pi(x) 為 矩形函式，則 Pi(x) 的 傅立葉變換 是 sinc 函式

F_x[Pi(x)](k)=sinc(pik).
(13)

因此，sinc 函式經常出現在物理應用中，例如傅立葉變換光譜學中，作為所謂的 儀器函式，它給出了儀器對 delta 函式 輸入的響應。從最終光譜中去除儀器函式需要使用某種 反捲積 演算法。

sinc 函式可以寫成複數 積分，注意到，對於 x!=0,

sinc(nx)=(sin(nx))/(nx)
(14)
=1/(nx)(e^(inx)-e^(-inx))/(2i)
(15)
=1/(2inx)[e^(itx)]_(-n)^n
(16)
=1/(2n)int_(-n)^ne^(ixt)dt,
(17)

並且對於 x=0，sinc(nx) 和積分都等於 1。

sinc 函式也可以寫成 無窮乘積

sinc(x)=product_(k=1)^inftycos(x/(2^k)),
(18)

這是 François Viète 在 1593 年發現的結果 (Kac 1959, Morrison 1995)，有時被稱為尤拉公式 (Prudnikov et al. 1986, p. 757; Gearhart and Shulz 1990)。它也由下式給出

sinc(x)=product_(k=1)^infty(1-(x^2)/(k^2pi^2))
(19)

(Gearhart and Shulz 1990) 和

sinc(x)=product_(k=1)^infty[1-4/3sin^2(x/(3^k))]
(20)

(Prudnikov et al. 1986, p. 757)。

另一個乘積由下式給出

product_(k=1)^(infty)sinc((2pi)/(2k+1))=pi/(2K)
(21)
=0.1805504...
(22)

(OEIS A118253; Prudnikov et al. 1986, p. 757)，其中 K=8.700... 是來自 多邊形外切 的常數。

正整數上的 sinc(k) 冪的和包括

sum_(k=1)^(infty)sinc(k)=-1/2+1/2pi
(23)
sum_(k=1)^(infty)sinc^2(k)=-1/2+1/2pi
(24)
sum_(k=1)^(infty)sinc^3(k)=-1/2+3/8pi
(25)
sum_(k=1)^(infty)sinc^4(k)=-1/2+1/3pi
(26)
sum_(k=1)^(infty)sinc^5(k)=-1/2+(115)/(384)pi
(27)
sum_(k=1)^(infty)sinc^6(k)=-1/2+(11)/(40)pi.
(28)

sinc(k) 和 sinc(k)^2 的和相等這個驚人的事實似乎最早發表在 Baillie (1978) 中。令人驚訝的是，這些和等於 -1/2 加上 pi 的有理倍數的模式在冪 n=7 時被打破，此時和等於

sum_(k=1)^inftysinc^7(k)=-1/2+P(x),
(29)

其中

P(x)=1/(46080)pi(129423-201684pi+144060pi^2-54880pi^3+11760pi^4-1344pi^5+64pi^6).
(30)

sinc 函式滿足恆等式

int_(-infty)^inftysinc[pi(x-y)]sinc(piy)dy=sinc(pix).
(31)

涉及 sinc 函式的定積分包括

int_0^inftysinc(x)dx=1/2pi
(32)
int_0^inftysinc^2(x)dx=1/2pi
(33)
int_0^inftysinc^3(x)dx=3/8pi
(34)
int_0^inftysinc^4(x)dx=1/3pi
(35)
int_0^inftysinc^5(x)dx=(115)/(384)pi.
(36)

在除以常數因子 pi 後，這些值再次為 1/2、1/2、3/8、1/3、115/384、11/40、5887/23040、151/630、259723/1146880、... (OEIS A049330 和 A049331; Grimsey 1945, Medhurst and Roberts 1965)。這些都是驚人的通用結果的特例

int_0^infty(sin^ax)/(x^b)dx=(pi^(1-c)(-1)^(|_(a-b)/2_|))/(2^(a-c)(b-1)!)sum_(k=0)^(|_a/2_|-c)(-1)^k(a; k)(a-2k)^(b-1)[ln(a-2k)]^c,
(37)

其中 a 和 b 是 正整數，使得 a>=b>c，c=a-b (mod 2)，|_x_| 是 向下取整函式，並且 0^0 被視為等於 1 (Kogan; 參見 Espinosa 和 Moll 2000)。當 n 是 正 偶數 整數時，這個壯觀的公式簡化為特殊情況

int_0^infty(sin^(2n)x)/(x^(2n))dx=pi/(2(2n-1)!)<2n-1; n-1>,
(38)

其中 <n; k> 是 尤拉數 (Kogan; 參見 Espinosa 和 Moll 2000)。積分的解也可以用係數的 遞推關係 來表示

c(a,b)={pi/(2^(a+1-b))(a-1; 1/2(a-1)) for b=1 or b=2; (a[(a-1)c(a-2,b-2)-a·c(a,b-2)])/((b-1)(b-2)) otherwise.
(39)
SincContour

可以使用 輪廓積分 推匯出 sinc(x) 的半無窮積分。在上圖中，考慮路徑 gamma=gamma_1+gamma_(12)+gamma_2+gamma_(21)。現在寫 z=Re^(itheta)。在弧線上，dz=iRe^(itheta)dtheta，在 x 軸 上，dz=e^(itheta)dR。寫

int_(-infty)^inftysinc(x)dx=Iint_gamma(e^(iz))/zdz,
(40)

其中 I 表示 虛部。現在定義

I=int_(-infty)^infty(e^(iz))/zdz
(41)
=lim_(R_1->0)int_pi^0(exp(iR_1e^(itheta)))/(R_1e^(itheta))iR_1e^(itheta)dtheta+lim_(R_1->0)lim_(R_2->infty)int_(R_1)^(R_2)(e^(iR))/RdR+lim_(R_2->infty)int_0^pi(exp(iz))/zdz+lim_(R_1->0; R_2->infty)int_(R_2)^(R_1)(e^(-iR))/(-R)(-dR),
(42)

其中第二項和第四項使用了恆等式 e^(i0)=1 和 e^(ipi)=-1。簡化後，

I=lim_(R_1->0)int_pi^0exp(iR_1e^(itheta))idtheta+int_(0^+)^infty(e^(iR))/RdR+lim_(R_2->infty)int_0^pi(exp(iz))/zdz+int_infty^(0^+)(e^(-iR))/(-R)(-dR)
(43)
=-int_0^piidtheta+int_(0^+)^infty(e^(iR))/RdR+0+int_(-infty)^(0^-)(e^(iR))/RdR,
(44)

其中第三項透過 約爾當引理 消失。對第一項進行積分並組合其他項得到

I=-ipi+int_(-infty)^infty(e^(iz))/zdz=0.
(45)

重新排列得到

int_(-infty)^infty(e^(iz))/zdz=ipi,
(46)

因此

int_(-infty)^infty(sinz)/zdz=pi.
(47)

透過注意，使用 復殘數 方法也得到了相同的結果

I=0+1/22piiRes_(z=0)f(z)
(48)
=ipi(z-0)(e^(iz))/z|_(z=0)
(49)
=ipi[e^(iz)]_(z=0)
(50)
=ipi,
(51)

因此

I(I)=pi.
(52)

由於被積函式是對稱的，因此我們有

int_0^infty(sinx)/xdx=1/2pi,
(53)

給出在 0 處評估的 正弦積分 為

si(0)=-int_0^infty(sinx)/xdx=-1/2pi.
(54)

另請參見

Borwein 積分、傅立葉變換、傅立葉變換--矩形函式、儀器函式、Jinc 函式、Kilroy 曲線、正弦、正弦積分、Sinhc 函式、Tanc 函式

使用 探索

參考文獻

Baillie, R. "Advanced Problem 6241." Amer. Math. Monthly 85, 828, 1978.Baillie, R.; Henrici, P.; and Johnsonbaugh, R. "Solution to Advanced Problem 6241." Amer. Math. Monthly 87, 496-498, 1980.Bracewell, R. "The Filtering or Interpolating Function, sincx." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 62-64, 1999.Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.Espinosa, O. and Moll, V. H. "On Some Definite Integrals Involving the Hurwitz Zeta Function." https://arxiv.org/abs/math/0012078. 11 Dec 2000.Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.Gearhart, W. B. and Schulz, H. S. "The Function sinx/x." College Math. J. 21, 90-99, 1990. http://www.maa.org/pubs/Calc_articles/ma003.pdf.Grimsey, A. H. R. "On the Accumulation of Chance Effects and the Gaussian Frequency Distribution." Phil. Mag. 36, 294-295, 1945.Higgins, J. R. "Five Short Stories About the Cardinal Series." Bull. Amer. Math. Soc. 12, 45-89, 1985.Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Washington, DC: Math. Assoc. Amer., 1959.Kogan, S. "A Note on Definite Integrals Involving Trigonometric Functions." Unpublished manuscript, n.d.McNamee, J.; Stenger, F.; and Whitney, E. L. "Whittaker's Cardinal Function in Retrospect." Math. Comput. 25, 141-154, 1971.Medhurst, R. G. and Roberts, J. H. "Evaluation of the Integral I_n(b)=(2/pi)int_0^infty(sinx/x)^ncos(bx)dx." Math. Comput. 19, 113-117, 1965.Morrison, K. E. "Cosine Products, Fourier Transforms, and Random Sums." Amer. Math. Monthly 102, 716-724, 1995.Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.Sloane, N. J. A. Sequences A049330, A049331, and A118253 in "The On-Line Encyclopedia of Integer Sequences."Stenger, F. Numerical Methods Based on Sinc and Analytic Functions. New York: Springer-Verlag, 1993.Woodward, P. M. Probability and Information Theory with Applications to Radar. New York: McGraw-Hill, 1953.Zimmermann, P. "Int(sin(x)^k/x^k,x=0..infinity)." math-fun@cs.arizona.edu posting, 4 Mar 1997.

在 上被引用

Sinc 函式

請引用為

Weisstein, Eric W. "Sinc 函式。" 來自 Web 資源。 https://mathworld.tw/SincFunction.html

學科分類