最常見的“正弦積分”定義為
 |
(1)
|
 是在 Wolfram 語言 中實現的函式,函式名為SinIntegral[z]。
是在 Wolfram 語言 中實現的函式,函式名為SinIntegral[z]。
 是一個 整函式。
是一個 整函式。
一個密切相關的函式定義為
其中  是 指數積分,(3) 對
是 指數積分,(3) 對  成立,並且
成立,並且
 |
(6)
|
導數  是
是
 |
(7)
|
其中  是 sinc 函式,積分 是
是 sinc 函式,積分 是
 |
(8)
|
對於  的級數由下式給出
的級數由下式給出
 |
(9)
|
(Havil 2003, p. 106)。
它可以用 第一類球貝塞爾函式 展開,形式為
![Si(2x)=2xsum_(n=0)^infty[j_n(x)]^2](/images/equations/SineIntegral/NumberedEquation6.svg) |
(10)
|
(Harris 2000)。
sinc 函式的半無限積分由下式給出
 |
(11)
|
要計算正弦函式乘以冪的積分
 |
(12)
|
使用 分部積分法。設
 |
(13)
|
 |
(14)
|
所以
 |
(15)
|
再次使用 分部積分法,
 |
(16)
|
 |
(17)
|
![intx^(2n)sin(mx)dx=-1/mx^(2n)cos(mx)
+(2n)/m[1/mx^(2n-1)cos(mx)-(2n-1)/mintx^(2n-2)sin(mx)dx]
=-1/mx^(2n)sin(mx)+(2n)/(m^2)x^(2n-1)sin(mx)-((2n)(2n-1))/(m^2)intx^(2n-2)sin(mx)dx
=-1/mx^(2n)cos(mx)+(2n)/(m^2)x^(2n-1)sin(mx)+...+((2n)!)/(m^(2n))intx^0sin(mx)dx
=-1/mx^(2n)cos(mx)+(2n)/(m^2)x^(2n-1)sin(mx)+...-((2n)!)/(m^(2n+1))cos(mx)
=cos(mx)sum_(k=0)^n(-1)^(k+1)((2n)!)/((2n-2k)!m^(2k+1))x^(2n-2k)
+sin(mx)sum_(k=1)^n(-1)^(k+1)((2n)!)/((2k-2n-1)!m^(2k))x^(2n-2k+1).](/images/equations/SineIntegral/NumberedEquation14.svg) |
(18)
|
令  ,所以
,所以
![intx^(2n)sin(mx)dx
=cos(mx)sum_(k=0)^n(-1)^(n-k+1)((2n)!)/((2k)!m^(2n-2k+1))x^(2k)+sin(mx)sum_(k=0)^(n-1)(-1)^(n-k+1)((2n)!)/((2k-1)!m^(2n-2k))x^(2k+1)
=(-1)^(n+1)(2n)![cos(mx)sum_(k=0)^n((-1)^k)/((2k)!m^(2n-2k+1))x^(2k)+sin(mx)sum_(k=1)^n((-1)^(k+1))/((2k-3)!m^(2n-2k+2))x^(2k-1)].](/images/equations/SineIntegral/NumberedEquation15.svg) |
(19)
|
形式為的一般積分
 |
(20)
|
與 sinc 函式 相關,並且可以解析計算。
另請參閱
Chi,
餘弦積分,
指數積分,
尼爾森螺線,
Shi,
Sinc 函式
相關的 Wolfram 網站
http://functions.wolfram.com/GammaBetaErf/SinIntegral/
使用 探索
參考文獻
Abramowitz, M. 和 Stegun, I. A. (編輯). "Sine and Cosine Integrals." §5.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 231-233, 1972.Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 342-343, 1985.Harris, F. E. "Spherical Bessel Expansions of Sine, Cosine, and Exponential Integrals." Appl. Numer. Math. 34, 95-98, 2000.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 105-106, 2003.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "Fresnel Integrals, Cosine and Sine Integrals." §6.79 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 248-252, 1992.Spanier, J. 和 Oldham, K. B. "The Cosine and Sine Integrals." Ch. 38 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 361-372, 1987.在 中引用
正弦積分
請引用為
Weisstein, Eric W. “正弦積分。” 來自 —— 資源。 https://mathworld.tw/SineIntegral.html
主題分類
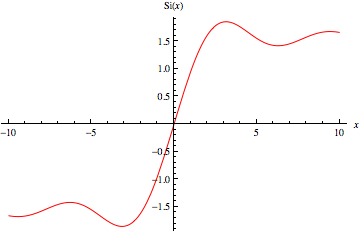
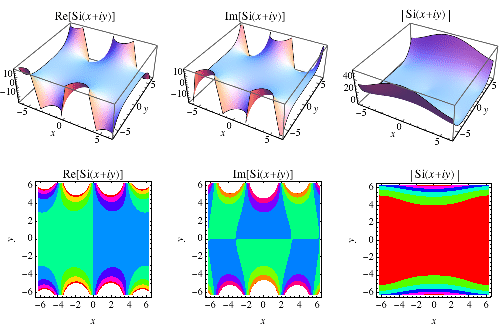
是在 Wolfram 語言 中實現的函式,函式名為SinIntegral[z]。
是一個 整函式。
是
的級數由下式給出

![intx^(2n)sin(mx)dx=-1/mx^(2n)cos(mx)
+(2n)/m[1/mx^(2n-1)cos(mx)-(2n-1)/mintx^(2n-2)sin(mx)dx]
=-1/mx^(2n)sin(mx)+(2n)/(m^2)x^(2n-1)sin(mx)-((2n)(2n-1))/(m^2)intx^(2n-2)sin(mx)dx
=-1/mx^(2n)cos(mx)+(2n)/(m^2)x^(2n-1)sin(mx)+...+((2n)!)/(m^(2n))intx^0sin(mx)dx
=-1/mx^(2n)cos(mx)+(2n)/(m^2)x^(2n-1)sin(mx)+...-((2n)!)/(m^(2n+1))cos(mx)
=cos(mx)sum_(k=0)^n(-1)^(k+1)((2n)!)/((2n-2k)!m^(2k+1))x^(2n-2k)
+sin(mx)sum_(k=1)^n(-1)^(k+1)((2n)!)/((2k-2n-1)!m^(2k))x^(2n-2k+1).](/images/equations/SineIntegral/NumberedEquation14.svg)
,所以
![intx^(2n)sin(mx)dx
=cos(mx)sum_(k=0)^n(-1)^(n-k+1)((2n)!)/((2k)!m^(2n-2k+1))x^(2k)+sin(mx)sum_(k=0)^(n-1)(-1)^(n-k+1)((2n)!)/((2k-1)!m^(2n-2k))x^(2k+1)
=(-1)^(n+1)(2n)![cos(mx)sum_(k=0)^n((-1)^k)/((2k)!m^(2n-2k+1))x^(2k)+sin(mx)sum_(k=1)^n((-1)^(k+1))/((2k-3)!m^(2n-2k+2))x^(2k-1)].](/images/equations/SineIntegral/NumberedEquation15.svg)