反餘切

	最小值	最大值
實部
虛部

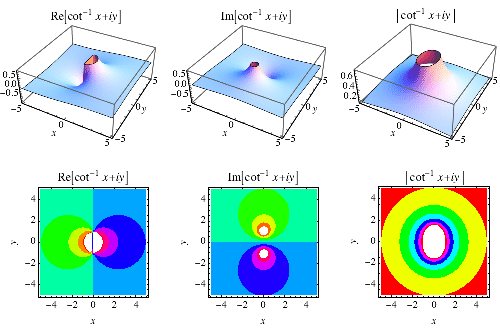
反餘切是多值函式 (Zwillinger 1995, p. 465)，也表示為 (Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 311; Jeffrey 2000, p. 124) 或 (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127)，它是餘切的反函式。變體 (例如，Beyer 1987, p. 141; Bronshtein and Semendyayev, 1997, p. 70) 和有時用於指代反餘切的顯式主值，儘管這種區分並不總是被做出 (例如，Zwillinger 1995, p. 466)。更糟糕的是，符號有時用於主值，而用於多值函式 (Abramowitz and Stegun 1972, p. 80)。請注意，在符號 (在北美和全球袖珍計算器中常用) 中，是餘切，而上標表示反函式，不是乘法逆元。

反餘切的主值在 Wolfram 語言中實現為ArcCot[z].

定義反餘切至少有兩種可能的約定。這項工作遵循 Abramowitz 和 Stegun (1972, p. 79) 以及 Wolfram 語言的約定，取的範圍為，在處不連續，並且分支切割線段沿著放置。這個定義可以用自然對數表示為

(1)

正如它必須的那樣，這個定義也與 Wolfram 語言對以下項的定義一致ArcTan，因此ArcCot[z] 等於ArcTan[1/z].

另一種不同但常見的約定 (例如，Zwillinger 1995, p. 466; Bronshtein and Semendyayev, 1997, p. 70; Jeffrey 2000, p. 125) 將的範圍定義為，從而給出一個在實數線上連續的函式。在檢查涉及反三角函式的恆等式時，應格外小心，因為它們的適用範圍或精確形式可能因所使用的約定而異。

的導數由下式給出

(2)

積分由下式給出

(3)

當時，反餘切的麥克勞林級數由下式給出

			(4)
			(5)

(OEIS A005408)。關於的洛朗級數由下式給出

			(6)
			(7)

對於。

尤拉推匯出了無窮級數

(8)

(Wetherfield 1996).

反餘切滿足

(9)

對於，

(10)

對於所有，並且

		${sec^(-1)((sqrt(x^2+1))/x)-pi for x<0; sec^(-1)((sqrt(x^2+1))/x) for x>0$	(11)
		${-1/2pi-tan^(-1)x for x<0; 1/2pi-tan^(-1)x for x>=0$	(12)
		${-sin^(-1)(1/(sqrt(x^2+1))) for x<0; sin^(-1)(1/(sqrt(x^2+1))) for x>0$	(13)
		${-1/2pi-cot^(-1)(1/x) for x<0; 1/2pi-cot^(-1)(1/x) for x>0$	(14)
		${-csc^(-1)(sqrt(x^2+1)) for x<0; csc^(-1)(sqrt(x^2+1)) for x>0$	(15)
		${cos^(-1)(x/(sqrt(x^2+1)))-pi for x<0; cos^(-1)(x/(sqrt(x^2+1))) for x>0$	(16)
		${-1/2pi-sin^(-1)(x/(sqrt(x^2+1))) for x<0; 1/2pi-sin^(-1)(x/(sqrt(x^2+1))) for x>0.$	(17)

餘切的解析和包括以下優美的結果

(18)

(OEIS A091007)，其中

(19)

(H. S. Wilf, pers. comm., May 21, 2002).

一個數

(20)

其中是一個整數或有理數，有時被稱為格雷果裡數。Lehmer (1938a) 表明，可以表示為整數引數的反餘切的有限和

(21)

其中

(22)

其中是向下取整函式，並且

			(23)
			(24)

其中且，並且遞迴持續到。如果一個反正切和寫成

(25)

那麼方程 (◇) 變為

(26)

其中

(27)

反餘切和可以用於生成類馬欽公式。

其他反餘切恆等式包括

			(28)
			(29)

以及許多其他恆等式 (Bennett 1926, Lehmer 1938b)。請注意，對於方程 (29)，的約定選擇很重要，因為它在約定中對所有複數成立，但在約定中，僅在以原點為中心的透鏡形區域之外成立。

另請參閱

餘切, 反餘割, 反餘弦, 反正割, 反正弦, 反正切, 反三角函式, Lehmer 餘切展開, 馬欽公式, 類馬欽公式, 正切

使用探索

更多嘗試

參考文獻

Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.Bennett, A. A. "The Four Term Diophantine Arccotangent Relation." Ann. Math. 27, 21-24, 1926.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, p. 70, 1997.Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 311, 1998.Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.Lehmer, D. H. "A Cotangent Analogue of Continued Fractions." Duke Math. J. 4, 323-340, 1938a.Lehmer, D. H. "On Arccotangent Relations for

." Amer. Math. Monthly 45, 657-664, 1938b.Sloane, N. J. A. Sequences A005408/M2400 and A091007 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.Wetherfield, M. "The Enhancement of Machin's Formula by Todd's Process." Math. Gaz. 80, 333-344, 1996.Zwillinger, D. (Ed.). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 465-467, 1995.

在中被引用

反餘切

請這樣引用

Weisstein, Eric W. “反餘切。” 來自 Web 資源。 https://mathworld.tw/InverseCotangent.html

反餘切

另請參閱

相關 Wolfram 網站

使用探索

參考文獻

在中被引用

請這樣引用

主題分類

反餘切

另請參閱

相關 Wolfram 網站

使用 探索

參考文獻

在 中被引用

請這樣引用

主題分類

使用探索

在中被引用