反餘弦是 多值函式 餘弦 的 反函式 。變體 主值 ,儘管這種區分並不總是明確 (例如,Zwillinger 1995, p. 466)。更糟糕的是,符號 餘弦 ,而上標 反函式 ,而不是乘法逆元。
反餘弦的 主值 在 Wolfram 語言 中實現為ArcCos z ],在 Wolfram 語言 中。在 GNU C 庫中,它被實現為acos (double x )。
反餘弦是 多值函式 ,因此在 複平面 中需要 分支切割 ,Wolfram 語言 的約定將其放置線上段
(1)
特殊值包括
導數
(5)
其 不定積分 是
(6)
反餘弦滿足
(7)
對於所有複數
(8)
反餘弦可以用其他反三角函式表示為
對於所有複數
(11)
對於
(12)
對於
對於
反餘弦的 麥克勞林級數 ,對於
(OEIS A055786 和 A002595 )。
另請參閱 餘弦 ,
反餘割 ,
反餘切 ,
反正弦 ,
反正割 ,
反正切 ,
反三角函式
相關 Wolfram 網站 http://functions.wolfram.com/ElementaryFunctions/ArcCos/
使用 探索
參考文獻 Abramowitz, M. and Stegun, I. A. (編). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. Apostol, T. M. Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. GNU C Library. "Mathematics: Inverse Trigonometric Functions." http://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC389 . Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Sloane, N. J. A. Sequences A002595 /M4233 和 A055786 in "The On-Line Encyclopedia of Integer Sequences." Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Zwillinger, D. (編). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae. 在 中被引用 反餘弦
請引用為
Weisstein, Eric W. "反餘弦。" 來自 https://mathworld.tw/InverseCosine.html
主題分類
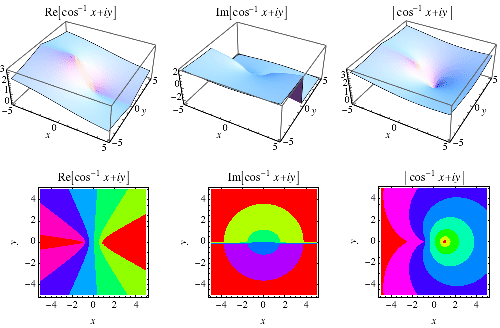
(Zwillinger 1995, p. 465),也記作
(Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 307; Jeffrey 2000, p. 124),它是 餘弦 的 反函式。變體
(例如,Beyer 1987, p. 141; Bronshtein and Semendyayev, 1997, p. 69) 和
有時用於指代反餘弦的顯式 主值,儘管這種區分並不總是明確 (例如,Zwillinger 1995, p. 466)。更糟糕的是,符號
有時用於主值,而
用於多值函式 (Abramowitz and Stegun 1972, p. 80)。請注意,符號
(在北美和全球袖珍計算器中常用)、
是 餘弦,而上標
表示 反函式,而不是乘法逆元。
和
上。這源於
的定義為
由下式給出
,以及

,
,

,以及



,其中在最後一個等式中,零處的等號被理解為在極限
下成立。
是
