主題
Search

Dedekind Eta 函式

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
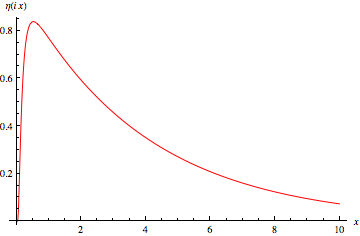
DedekindEtaReal
最小值 最大值
Powered by webMathematica

Dedekind eta 函式定義在上半平面 H={tau:I[tau]>0} 上，由下式給出

eta(tau)=q^_^(1/24)(q^_)_infty
(1)
=q^_^(1/24)product_(k=1)^(infty)(1-q^_^k)
(2)
=q^_^(1/24)sum_(n=-infty)^(infty)(-1)^nq^_^(n(3n-1)/2)
(3)
=sum_(n=-infty)^(infty)(-1)^nq^_^((6n-1)^2/24)
(4)
=q^_^(1/24){1+sum_(n=1)^(infty)(-1)^n[q^_^(n(3n-1)/2)+q^_^(n(3n+1)/2)]}
(5)
=q^_^(1/24)(1-q^_-q^_^2+q^_^5+q^_^7-q^_^(12)-...)
(6)

(OEIS A010815), 其中 q^_=e^(2piitau) 是 nome nome q 的平方, tau 是半週期比 half-period ratio, 並且 (q)_infty 是一個 q-級數 q-series (Weber 1902, pp. 85 and 112; Atkin and Morain 1993; Berndt 1994, p. 139)。

Dedekind eta 函式在 Wolfram 語言 中實現為DedekindEta[tau]。

用 q^_ 顯式地用半週期比 half-period ratio tau 重寫定義，得到乘積

eta(tau)=e^(piitau/12)product_(k=1)^infty(1-e^(2piiktau)).
(7)
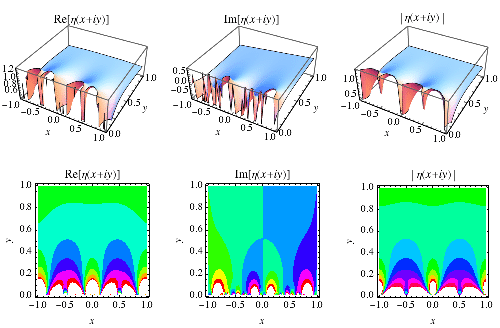DedekindEtaReImAbs
最小值 最大值
Re
Im Powered by webMathematica

它在上面的複平面 complex plane 中進行了說明。

eta(tau) 是由 Dedekind 在 1877 年首次引入的模形式 modular form，並且與 Weierstrass 橢圓函式 Weierstrass elliptic function 的模判別式 modular discriminant 相關，關係如下：

Delta(tau)=(2pi)^(12)[eta(tau)]^(24)
(8)

(Apostol 1997, p. 47)。

導數的緊湊閉合形式由下式給出

(deta(tau))/(dtau)=i/pieta(tau)zeta(1;g_2,g_3),
(9)

其中 zeta(z;g_2,g_3) 是 Weierstrass zeta 函式 Weierstrass zeta function，g_2 和 g_3 是對應於半週期 (1,tau) 的不變數。 eta(tau) 的導數滿足

-4piid/(dtau)ln[eta(tau)]=G_2(tau),
(10)

其中 G_2(tau) 是 Eisenstein 級數 Eisenstein series，並且

d/(dtau)ln[eta(-1/tau)]=d/(dtau)ln[eta(tau)]+1/2d/(dtau)ln(-itau).
(11)

一個特殊值由下式給出

eta(i)=(Gamma(1/4))/(2pi^(3/4))
(12)
=0.7682254...
(13)

(OEIS A091343), 其中 Gamma(z) 是 gamma 函式 gamma function。 另一個特殊情況是

P=(x^3-x-1)_1
(14)
=(e^(ipi/24)eta(tau_0))/(sqrt(2)eta(2tau_0))
(15)
=1.3247179572...
(16)

其中 P 是塑性常數 plastic constant，(P(x))_n 表示多項式根 polynomial root，並且 tau_0=(1+isqrt(23))/2。

令 zeta_(24)=e^(2pii/24)=e^(pii/12) 為單位根 root of unity，eta(tau) 滿足

eta(tau+1)=zeta_(24)eta(tau)
(17)
eta(tau+n)=zeta_(24)^neta(tau)
(18)
eta(-1/tau)=sqrt(-itau)eta(tau)
(19)

其中 n 是一個整數 (Weber 1902, p. 113; Atkin and Morain 1993; Apostol 1997, p. 47)。 Dedekind eta 函式與 Jacobi theta 函式 Jacobi theta function theta_2 相關，關係如下：

eta(q^_)=(theta_2(1/6pi,q^_^(1/6)))/(sqrt(3))
(20)

(Weber 1902, Vol. 3, p. 112) 和

theta_3(0,e^(piitau))=(eta^2(1/2(tau+1)))/(eta(tau+1))
(21)

(Apostol 1997, p. 91)。

Macdonald (1972) 將大多數 形式為 (q,q)_infty^c 的展開式與仿射根系 root systems 聯絡起來。 Macdonald 的處理中未包含的例外情況包括 Hecke 和 Rogers 發現的 c=2, Ramanujan 發現的 c=4, 以及 Atkin 發現的 c=26 (Leininger and Milne 1999)。 使用 Dedekind eta 函式，Jacobi 三重積 Jacobi triple product 恆等式

(q,q)_infty^3=sum_(n=0)^infty(-1)^n(2n+1)q^(n(n+1)/2)
(22)

可以寫成

eta^3(tau)=sum_(n=0)^infty(-1)^n(2n+1)q^_^((2n+1)^2/8)
(23)

(Jacobi 1829, Hardy and Wright 1979, Hirschhorn 1999, Leininger and Milne 1999)。

Dedekind 的函式方程指出，如果 [a b; c d] in Gamma，其中 Gamma 是模群 Gamma modular group Gamma，c>0，並且 tau in H (其中 H 是上半平面 upper half-plane)，那麼

eta((atau+b)/(ctau+d))=epsilon(a,b,c,d)[sqrt(-i(ctau+d))]eta(tau),
(24)

其中

epsilon(a,b,c,d)=exp[pii((a+d)/(12c)+s(-d,c))],
(25)

並且

s(h,k)=sum_(r=1)^(k-1)r/k((hr)/k-|_(hr)/k_|-1/2)
(26)

是 Dedekind 和 Dedekind sum (Apostol 1997, pp. 52-57)，其中 |_x_| 是向下取整函式 floor function。

參見

Dirichlet Eta 函式, Dedekind 和, 橢圓不變數, 橢圓 Lambda 函式, 無窮乘積, Jacobi Theta 函式, Klein 絕對不變數, q-乘積, q-級數, Rogers-Ramanujan 連分式, Tau 函式, Weber 函式

相關 Wolfram 網站

http://functions.wolfram.com/EllipticFunctions/DedekindEta/

使用 探索

參考文獻

Apostol, T. M. "The Dedekind Eta Function." Ch. 3 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 47-73, 1997.Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.Bhargava, S. and Somashekara, D. "Some Eta-Function Identities Deducible from Ramanujan's _1psi_1 Summation." J. Math. Anal. Appl. 176, 554-560, 1993.Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.Jacobi, C. G. J. Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, p. 90, 1829.Leininger, V. E. and Milne, S. C. "Expansions for (q)_infty^(n^2+n) and Basic Hypergeometric Series in U(n)." Discr. Math. 204, 281-317, 1999a.Leininger, V. E. and Milne, S. C. "Some New Infinite Families of eta-Function Identities." Methods Appl. Anal. 6, 225-248, 1999b.Köhler, G. "Some Eta-Identities Arising from Theta Series." Math. Scand. 66, 147-154, 1990.Macdonald, I. G. "Affine Root Systems and Dedekind's eta-Function." Invent. Math. 15, 91-143, 1972.Ramanujan, S. "On Certain Arithmetical Functions." Trans. Cambridge Philos. Soc. 22, 159-184, 1916.Siegel, C. L. "A Simple Proof of eta(-1/tau)=eta(tau)sqrt(tau/i)." Mathematika 1, 4, 1954.Sloane, N. J. A. Sequences A010815, A091343, and A116397 in "The On-Line Encyclopedia of Integer Sequences."Weber, H. Lehrbuch der Algebra, Vols. I-III. 1902. Reprinted as Lehrbuch der Algebra, Vols. I-III, 3rd rev ed. New York: Chelsea, 1979.

在 中被引用

Dedekind Eta 函式

引用為

Weisstein, Eric W. "Dedekind Eta 函式。" 來自 Web 資源。 https://mathworld.tw/DedekindEtaFunction.html

主題分類